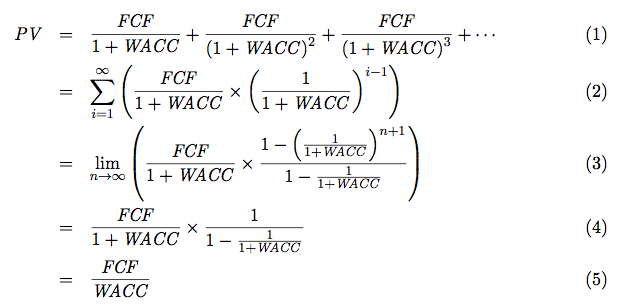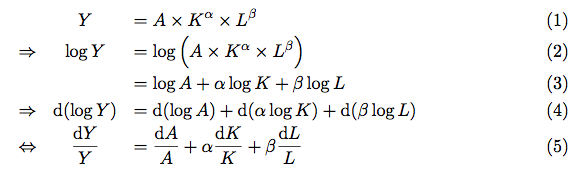[1次2次] 理系のための診断士学習法（#1）

中小企業診断士を目指す皆様、おはようございます。
がんちゃん／岩間です。

診断士試験の学習では、色々な数式や数学的な概念が出てきます。試験対策の観点では結果を記憶するのも有効ですが、結果に至るまでの過程も押さえておくことで、理解が深まるという側面もあります。（その他には楽しく学習できるといった効果もあるかもしれません）

そこで、診断士試験で出題される数式や数学的な概念を見てみます。（今後、毎週月曜日の記事で何回か紹介します）

診断士対策のテキストや、予備校の講義で扱われない内容が多いので、見る価値あり！と思います。

本記事は、特に、お仕事で数式を良く使う方、学生時代にいわゆる理系だった方や文系で数学が得意だった方にお読みいただければと思います。

 

◆本記事の使い方

• 紹介するテーマのうち、興味があるものについてお読みいただければと思います。
  平易な説明を心がけますが、記事のスペース上、完全な解説はしていないため、適宜、キーワードを元に検索するなどで補完していただければ幸いです。
• 本記事中は、次の凡例を使います。
  • 緑色：数学に関する知識

 

◆目次

• １．[財務] DCF法の公式（簡易版）
• ２．[財務] DCF法の公式【数列】
• ３．[経済] コブ・ダグラス型生産関数の成長方程式／全要素生産性(TFP) 【対数・微分】

 

◆１．DCF法の公式【簡易版】

【DCF法とは】

• DCF法(Discounted Cash Flow Analysis)は、企業価値を算出する方法の一つです。
• これは、「その企業が毎年一定額のフリーキャッシュフローを永続的に得られること」を仮定し、そのフリーキャッシュフローの現在価値の総額を企業価値とするものです。
• 企業価値は、FCF÷WACC として求めます。 

【公式の導出方法】

この公式は簡易に導出することができます。まずはその方法を紹介します。

ポイントは、次のとおりです。

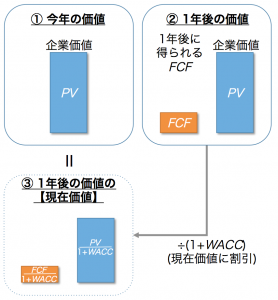
• 今年の企業価値は、1年後に減る（時間価値を考慮するため）(1)。
• 1年度にFCFを得られるので、1年後の企業価値が増える (2)。
• (1)で減った分と、(2)で増えた分が相殺され、今年の企業価値と、1年後の企業価値は同じ。

次のように導出します。

• 現在の企業価値をPVと置きます(①)
• 次に、1年後の状態を考えます(②)
  • 1年後時点での企業価値も、今年と同じPVです
  • 1年後にはFCFが得られます。
• 現在の企業価値(①)と1年後の状態の現在価値(③)は等しいですので、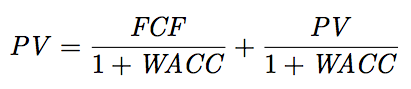となります。
• これをPVについて解くと、PV＝FCF÷WACCとなります(※)。

※解き方は、次のとおりです。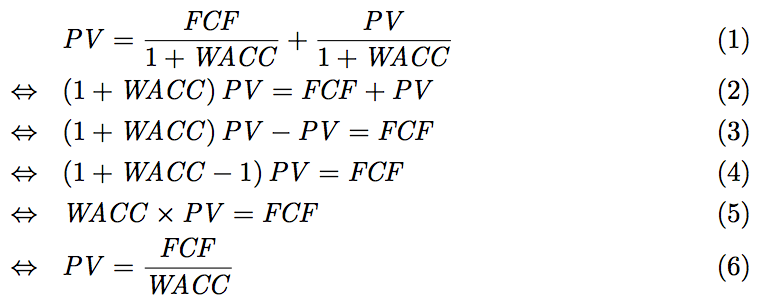
それぞれの式変形で行ったことは次のとおりです：

• (1)→(2)：両辺に1+WACCを掛ける
• (2)→(3)：両辺からPVを引く
• (3)→(4)：左辺をPVでくくる
• (4)→(5)：左辺の括弧内を計算
• (5)→(6)：両辺をWACCで割る

 

◆２．DCF法の公式【数列を使う】

１では、DCF法の公式を簡単に導出する方法を紹介しました。ここでは、より定義に忠実に沿った方法を紹介します。

企業価値は、「今後毎年得られるFCFの現在価値の総額」でした。
この定義に忠実に、企業価値(PV)を求めると、次のようになります。

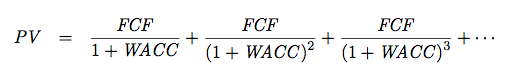
ここで使うのが、等比数列（等比級数・無限等比級数）という概念です。

【数列、等比数列、等比級数、無限等比級数に関する数学的知識】 数列とは、数を順番に並べた列のことです。数列の一種に、等比数列があります。これは、1, 0.5, 0.25, 0.125, … のように、隣り合う項の比が一定の数列です。 等比数列の各項は、と表されます（nは項の番号、rは隣り合う項の比） (上述の数列の場合、) 等比数列における1項目からn項目までの和は、等比級数と呼ばれ、と表されます。 (上述の数列の場合、） 等比数列における全ての項の和を、無限等比級数と呼びます。-1＜r＜1の場合に無限等比級数が収束し（値が定まり）、その値はとなります。（上述の数列の場合、1/(1−0.5)＝2）

これを使うと、企業価値の式が次のように求められます。 

それぞれの式変形で行ったことは次のとおりです：

• (1)→(2)：(1)の式を等比数列と見なし、等比数列の形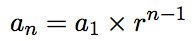（）で表記
• (2)→(3)：等比級数の和の式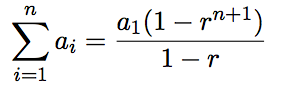（）で表記。
  (なお、limは、括弧内の数式に対して、nを正の無限大に近づけるという意味です)
• (3)→(4)：無限等比級数の式で表記（）
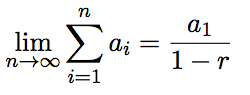• (4)→(5)：式を整理

 

◆３．コブ・ダグラス型生産関数の成長方程式／全要素生産性(TFP)【対数・微分】 

生産関数とは、生産量が、生産要素の投入量によってどのように変化するかを表す関数のことです。

コブ・ダグラス型生産関数とは、「生産量が、資本と労働によって決まる」という考え方に基づいた生産関数です。（設備を増強する（＝資本の増加）と生産力は向上しますし、従業員を増やす（＝労働の増加）と生産力は向上します。）
コブ・ダグラス型生産関数は、次のような式で表します。（AはTFP(Total Factor Productivity, 全要素生産性)と呼ばれる係数、Kは資本、Lは労働）

そして、これから、成長方程式という関係式を導けます。（dは変化を表します。Δと同義です）

この式では、全ての項が「d○/○」という「成長率」で表されていることがポイントです。すなわち、「生産量の成長率は、TFPの成長率と、資本の成長率と、労働の成長率で表される」ということになります。

 

この成長方程式の導出に使うのが、対数と微分の概念です。

【対数関数、対数関数の微分 に関する数学的知識】 対数関数とは、指数関数()の逆関数のことです。 xの対数を、log(x)と表します。 対数関数には、log(xy)＝log(x)＋log(y) という関係があります(※)。 log(x)の導関数（微分した関数）は、1/xです。（） ※これは、logに変換することによって、掛け算の形(xy)を足し算の形(logx+logy)で表せるということで、対数関数の大きな特徴です。

これを使うと、次のように、生産関数から成長方程式を導けます。 

それぞれの式変形で行ったことは次のとおりです：

• (1)→(2)：対数を取る
• (2)→(3)：対数内の積を和に変換（log(xy)＝log(x)＋log(y)の式を利用）
• (3)→(4)：各項を微分形式で表記
• (4)→(5)：対数関数の微分の公式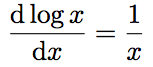（）を使って、各項を整理

 

 

---

 

2次筆記試験の結果発表がありました。

通過された方は、口述試験対策をしっかり行い、万全な体制で臨んでいただければと思います。（タキプロの過去の口述試験の記事をご参照ください）

通過されなかった方は、大変複雑な気持ちでいらっしゃるとお察しします。私自身が筆記試験を通過できなかった時は、数日間は何もやる気が起きず、好きなことをして過ごしました。その後、診断士を目指す意義を考えました。結果的には、意義は分からぬままでしたが、「諦めるのは早い」という考えに至り、結果的に再挑戦することを決めました。そしてそれから学習プランを立てました。
ご自身で納得のいく方法が見つかりますよう、願っています。

以上、がんちゃん／岩間 でした。

 

タキプロ 口述セミナー（東京）のお知らせ　※満員御礼※

---

おかげさまで募集定員に達しました。
お申し込みありがとうございました。

■日時
12月16日（火曜日）19:00～21:20（18:30開場）
大崎第二集会所（東京都品川区大崎2-9-4）

■定員：24名

■対象：２次筆記試験合格者

■参加費：無料（懇親会は3,500円程度）

■内容：口述試験の説明・模擬面接

■連絡事項
※12/13（土）に開催されたセミナーと同内容です。
※セミナー終了後、懇親会を予定しております。ぜひご参加ください。
※その他セミナーに関するお問い合わせは下記までお願いします。
タキプロ事務局：　takipro2010@gmail.com

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

皆様の応援がタキプロの原動力となります。
ぽちっと押して、応援お願いします♪

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝