[2次] (財務・会計) 押さえておくと安心。過去1～2回出題された論点

中小企業診断士を目指す皆様、おはようございます。がんちゃん／岩間です。

本日は、事例Ⅳで過去に1～2回だけ出題された計算が伴う論点を、説明します。

もしこれらの論点が出題されたときには、過去問に徹底的に取り組んだ方とそうでない方で、差がつきやすくなります。特にストレート生の方などあまり準備する時間がなかった方にとっては、これらのポイントを押さえておく効果は高いと思います。

少し長い記事になりますが、ぜひ学習の参考としてお読みいただければと思います。

なお、多少高度な論点には ★印（ピンク色） を付けていますので、財務・会計があまり得意ではない方は読み飛ばしていただければと思います。

 (10月6日 23:15に、2章に軽微な変更を加えました：ROA、ROE、負債利子率の大小関係について追記しました)

◆目次

1. 損益分岐点分析の高低点法 [H19第2問、H15第2問]
2. ROAとROEの関係、財務レバレッジ効果 [H21第2問]
3. 企業価値 [H24第3問、H16第3問]
4. 分散、標準偏差 [H21第2問、H14第4問]
5. 営業レバレッジ [H21第3問]

 

◆１．高低点法（損益分岐点分析）

ポイント 高低点法で、変動費率と固定費を算出できるようにしましょう。

過去問での出題：平成19年度 第2問、平成15年度 第2問

損益分岐点を求めるために必要な変動費率と固定費は、勘定科目ごとに変動費か固定費かを区分することにより算出する場合が多いです（勘定科目法と呼ばれます）。例えば「材料費は変動費で、その他は固定費とする」といった形です。

それ以外の方法として「2期分の売上高（あるいは操業度）と利益の実績から、変動費率と固定費を定める」という方法（高低点法）があります。

 

◇変動費率と固定費の求め方

高低点法で変動費率と固定費を算出するには、売上・費用のグラフを描くか、連立方程式を立てます。

例を見てみましょう。ある企業の2期分の売上高と利益が、次のとおりであったとし、2期で費用構造が変わらないものとします。

	第1期	第2期
売上高	100百万円	120百万円
利益	20百万円	30百万円

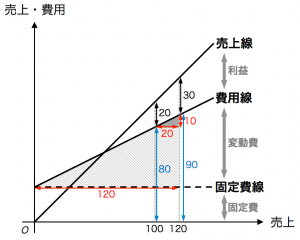
【売上・費用グラフを描く場合】(図1)

• 2期間で、売上が20（＝120−100）増えていて、利益が10（＝30−20）増えているため、変動費が10増えていることが分かります。
• 2期間で、売上が20増え、変動費が10増えていることから、変動費率は 10÷20＝50% となります。
• 1期目について、変動費は50（＝売上100×変動費率50%）で、利益が20なので、固定費は30（＝売上100−変動費50−利益20）です。

【連立方程式を立てる場合】

• 変動費率をα、固定費をFCとおきます。
• 売上高−売上高×α−FC＝利益 という式を2つ立てます。
  • [第1期] 100−100×α−FC＝20
  • [第2期] 120−120×α−FC＝30
• これを解いて、α＝0.5, FC＝30と求めます。

 

◆２．ROAとROEの関係、財務レバレッジ効果

ポイント 「ROAは、ROEと負債利子率の加重平均」という点を理解しましょう。 ⇒3つの大小関係は、ROE≦ROA≦負債利子率 か、負債利子率≦ROA≦ROE のいずれかです。 その上で、「ROA＜負債利子率なら、負債比率を減らせばROEは向上する」という点を理解しましょう。 ★ ROE＝ROA＋(ROA−負債利子率)×負債比率 という式を導出できると良いです。

過去問での出題：平成21年度 第2問

1次試験で「ROEとROAの関係式」を学習したと思いますが、複雑すぎて捨てていた方もいらっしゃるかもしれません。しかし、ひとたび理解してしまえば、直感にも合うため、理解することをお勧めします。

 

◇ROEとROAとは？

ROE、ROAの意味は次のとおりです。

• ROA：総資本（自己資本＋負債）に対してどれだけ(事業)利益を稼いだかを表す、利益率
• ROE：自己資本に対してどれだけ(純)利益を稼いだかを表す、利益率

併せて、負債利子率(i)の意味は次のとおりです。

• 負債利子率(i)は、負債に対して支払うべき利息の利子率です。

 

◇ROE・ROA・負債利子率の関係性：
「ROAはROEと負債利子率の平均」

一見、ROAとROEと負債利子率(i)は無関係のように見えますが、非常に強い関係があります。
⇒それは「ROAは、ROEと負債利子率(i)の平均である」ということです。正確には、ROAは、ROEとiを、対応する自己資本(E)と負債(D)で加重平均した値です。実際に計算してみると、その加重平均がROAと等しいことが分かります。

加重平均	＝	(ROE×E＋i×D)÷(E+D)
	＝	(純利益＋支払利息)÷総資産
	＝	事業利益÷総資産	＝	ROA

そのため、3つの大小関係は次のいずれかになります。いずれも平均であるROAが中央にきます(※)。

 

1.	ROE	≦	ROA	≦	負債利子率
2.	負債利子率	≦	ROA	≦	ROE

（※ 身近な例として、国語と算数の成績になぞらえて考えてみます。ROEを国語の得点、iを算数の得点、ROAを国語と算数の平均点と捉えてみます。国語(ROE)が50点で算数(i)が70点なら、平均(ROA)は60点で、国語(ROE)≦平均(ROA)≦算数(i)になります。逆に、国語(ROE)が70点で算数(i)が50点なら、平均(ROA)は60点で、算数(i)≦平均(ROA)≦国語(ROE)になります。いずれの場合も、平均が真ん中にきます）

 

◇ROEを高めるには負債比率をどう設定すべきか？

ROEを高めるのは経営的に重要な課題です。そのために「負債比率をどのように設定すべきか」を考えてみます。

ROA＜i だった場合には、ROEは、ROAやiより小さくなります。
⇒これは「せっかく事業利益をたくさん得ている(ROA)のに、負債の負担が大きい(i)ので、最終的な利益が小さい(ROE)」という状況です。
⇒この状況で、ROEを高めるには、負債の負担を減らすため、負債比率(D/E)を下げればよいと言えます。

ROA＞i だった場合は、上記議論の逆で、ROEを高めるには、相対的に安価な負債を活用するため、負債比率(D/E)を上げればよいと言えます。

 

◇★ ROE・ROA・負債利子率 の公式

1次で学習した ROE＝ROA＋(ROA－i)×D/E という公式も、前述の加重平均を表す式から算出できます。下に示すように、加重平均を表す式をROEについて解く（ROE＝…という式にする）だけです。数学が苦手でない方は、丸暗記するのではなく試験中に導出できるようにしておくことをお勧めします。

	ROA＝(ROE×E＋i×D)÷(E+D)	（加重平均を表す式）
⇔	ROA×(E+D)＝ROE×E＋i×D	（両辺にE＋Dを掛ける）
⇔	ROE＝ROA×(E+D)÷E－i×D÷E	（ROEを左にもってくる）
⇔	ROE＝ROA＋ROA×D÷E－i×D÷E	（右辺第1項を展開する）
⇔	ROE＝ROA＋(ROA－i)×D/E	（右辺第2項・第3項をくくる）

 

◆３．企業価値

ポイント 「企業価値＝FCF÷WACC」という式を覚えておきましょう(DCF法)。

過去問での出題：平成24年度 第3問、平成16年度 第3問

企業価値を算出する方法のうち、もっとも定番のものはDCF法(ディスカウンテッドキャッシュフロー法)です。これは、今後永続的に、毎年一定額のフリーキャッシュフローを得られることを仮定し、そのフリーキャッシュフローの現在価値を企業価値とするものです。

企業価値は、FCF÷WACC として求めます。

分母はWACCであって、1+WACC ではないことに注意しましょう。

また、企業価値の規模感覚として「企業価値＝毎期得られるCFの10～20倍」と認識しておくと良いです。これは、WACC＝5～10%として計算したものです。

 

◇ ★ 公式の簡単な導出方法

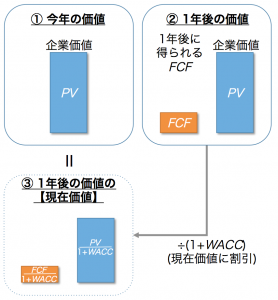
FCF÷WACCという式を丸暗記している方も多いと思いますが、簡単な導出方法を紹介します(図2)。試験中にも導出できる程度の簡易なものですので、数学が苦手でなければ、導出方法も理解しておくのをお勧めします。

• 現在の企業価値をPVと置きます(①)
• 次に、1年後の状態を考えます(②)
  • 1年後時点での企業価値も、今年と同じPVです（「これから毎年FCFが入ってくる」という条件が今年と変わらないため）
  • 1年後にはFCFが得られます。
• 現在の企業価値(①)と1年後の状態の現在価値(②)は等しいです(③)ので、PV＝FCF÷(1+WACC)＋PV÷(1+WACC) となり、
  これをPVについて解くと、PV＝FCF÷WACCとなります。
  

  	PV＝FCF÷(1＋WACC)＋PV÷(1+WACC)
  ⇔	(1＋WACC)PV＝FCF＋PV	（両辺に1＋WACCを掛ける）
  ⇔	(1＋WACC)PV−PV＝FCF	（両辺からPVを引く）
  ⇔	(1＋WACC−1)PV＝FCF	（左辺をPVでくくる）
  ⇔	WACC×PV＝FCF	（左辺の括弧内を計算）
  ⇔	PV＝FCF÷WACC	（両辺をWACCで割る）

 

◆４．分散・標準偏差

ポイント 分散と標準偏差の式を再確認しておきましょう。 分散は、「期待値との差」に着目します。 そして、「期待値との差」を2乗します。 標準偏差は、ルートを付けます。分散を求めるときに2乗した効果を元に戻すためです。

過去問での出題：平成21年度 第2問、平成14年度 第4問

 1次試験で、期待値、分散・標準偏差の概念を学んだと思います。期待値は覚えている方が多いと思いますが、分散や標準偏差までは覚えていますか？

定義は以下のとおりです。

この定義を理解するポイントは、次の3つです。

1. 分散は「期待値(平均値)との差」に着目します。
   ⇒ばらつきを測るためには、「基準」を定める必要があります。それには、全要素のちょうど中心の値である平均値を使います。
2. そのときに、2乗します。
   ⇒2乗する理由は、「中心から離れていればいるほど、ばらつきへの効果を大きくしたいため」と理解すると良いです(※)
3. 標準偏差は、分散にルートをつけます。
   ⇒分散を計算するときに2乗しました。しかし、これでは元の値と単位が異なってしまって、元の値と比較することができません。 (例えば、元の値がm(メートル)の単位なのに、分散がm²(平方メートル)となってしまうと、その分散が大きいのか小さいのか比べることができません)。ですので、単位を合わせて比較できるようにするために、ルートを付けます。

※★なぜ「期待値との差の2乗」とするか

敢えて「期待値との差の2乗」と定義しているのには理由があります。

• まずは「中心とのばらつきを見たいのだから、単純に[期待値との差]と定義すればよいのでは？」と思えます。しかし、そうしてしまうと、プラスのものもマイナスのものも出てきてしまい、足し合わせるとゼロになり、意味をなしません。
• それでは、「[期待値の差の絶対値]とすればよいのでは？」と思えます。しかし、「絶対値」は数学的にとても扱いにくい関数である（微分不可能な点を生じうる関数である）ため、偏差に「絶対値」を含めたくないという背景があります。仮に含めてしまうと、理論を発展させる弊害となってしまいます。
• そこで、次善の方法として、「期待値の差を2乗する」という方法が採られています。この定義であれば、中心とのばらつきを比較的簡単に扱えるからです。

 

◆５．営業レバレッジ 

ポイント 営業レバレッジは、「固定費の活用度合いを図る指標」です。 (固定費＋利益)÷利益 として算出します。 名前が似ている「財務レバレッジ」と対比して覚えましょう。 財務レバレッジは、「負債の活用度合いを図る指標」で、「(負債＋純資産)÷純資産」で算出します。 ★ 営業レバレッジ＝1÷安全余裕率 です。 ★ 本来的には、営業レバレッジは売上高に対する営業利益の弾力性として定義します。

過去問での出題：平成21年度 第3問

◇営業レバレッジとは

企業経営における固定費の活用度合いを図る指標です。

 

◇算出式

「(固定費＋利益)÷利益」という式で求めることができます。ここで、固定費＋利益は、限界利益のことで、同時に、「売上高－変動費」でもあります。

 

◇覚える際のコツ

営業レバレッジは、名前が似ている「財務レバレッジ」と対比させて覚えると良いです。財務レバレッジは、負債の活用度合いを図る指標で、「（負債＋純資産）÷純資産」と定義されます。

指標	活用度を測る対象	算出式
営業レバレッジ	固定費	(固定費＋利益)÷利益
財務レバレッジ	負債	(負債＋純資産)÷純資産

 

◇★営業レバレッジは安全余裕率の逆数です。

営業レバレッジは、「安全余裕率の逆数である」という性質があります。これを知っておけば、「営業レバレッジがどうなるか」を考えるには、「安全余裕率(の逆数)がどうなるか」を考えれば良いことが分かります。

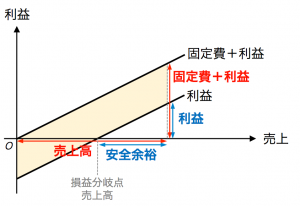
「安全余裕率の逆数」と一致する理由は、グラフで理解するのが容易です。図3は、利益と売上の関係を示したグラフです。ここで、利益の上に固定費(黄色)を積み上げています。図3から、安全余裕：利益＝売上高：固定費＋利益 となることが分かります(各々を2辺とする2つの直角3角形が相似だからです)。そのため、(固定費＋利益)÷利益＝売上高÷安全余裕＝1÷安全余裕率 となります。

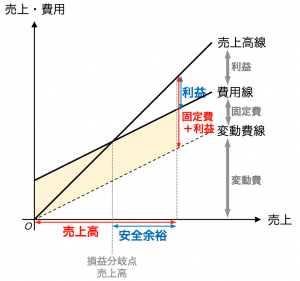
なお、図3と同様の議論を、見慣れている売上・費用グラフで表したものが、図4です。ただし、一般的な売上・費用グラフと比べて、変動費の上に固定費を積み上げている点が異なります。

図3と図4のどちらか理解しやすい方で理解いただければと思います。

 

◇★営業レバレッジの本来的な定義は、売上高に対する営業利益の弾力性です。

営業レバレッジは、本来的には「売上高（あるいは操業度）に対して、営業利益がどれだけ変化するか」を見る指標で、「売上高に対する営業利益の弾力性」と定義され、(Δ営業利益÷営業利益)÷(Δ売上高÷売上高) と算出します(※)。

※この式は、先ほどの定義の「(固定費＋利益)÷利益」と等価です。理由は次のように式変形できるからです。（以下、OP：営業利益(利益)、MP：限界利益、P：売上高、α：変動費率 とします）

	営業レバレッジ
＝	(ΔOP÷OP)÷(ΔP÷P)	定義より
＝	(ΔOP÷ΔP)÷(OP÷P)	乗除算の順序を変更
＝	(ΔMP÷ΔP)÷(OP÷P)	OP＋FC＝MP ⇒ ΔOP＋ΔFC＝ΔMP です。ここでΔFC＝0なので、ΔOP＝ΔMPです。
＝	(MP÷P)÷(OP÷P)	MP＝P×(1−α) ⇒ ΔMP＝ΔP×(1−α) です。これより、ΔMP÷ΔP＝MP÷P です。
＝	MP÷OP (限界利益÷営業利益)

 

◆まとめ

今日は、次の5点に関して説明しました。

1. 損益分岐点分析の高低点法 [H19第2問、H15第2問]
2. ROAとROEの関係、財務レバレッジ効果 [H21第2問]
3. 企業価値 [H24第3問、H16第3問]
4. 分散、標準偏差 [H14第4問、H21第2問]
5. 営業レバレッジ [H21第3問]

今日ご紹介した論点は、他の重要な論点（経営分析、CF、損益分岐点分析、投資判断など）と比べると、出題される可能性が高いとは言えません。しかし、これらの論点も記憶の片隅に置いておくことで、事例Ⅳを得点源にできる可能性が高まります。

とはいえ、これらの論点を押さえている受験生はそう多くはないと思われますので、もし難しいと感じたら、重要な論点に優先して取り組んでいただければと思います。

 

以上、がんちゃん／岩間 でした。

 

タキプロ勉強会のお知らせ

---

【東京勉強会】

＊各回定員5名 
＊参加費　500円 
少数ですが、ぜひ気軽にご参加ください。

・第8回　10/11（土）　9:30～12:20  昭和生涯学習センター
題材：H24事例Ⅳ　テーマ：提案力対策＆文章力対策

・第9回　10/13（月・祝）　9:30～12:20 西生涯学習センター
よろず相談所

＊題材の過去問を解いて、解答のコピーを6部 ご用意ください。 
＊時間の都合上、全部の設問を扱うことはできません。
あらかじめご了承願います。

お申込みはこちらから

 

【大阪勉強会】

◆場　所：グランフロント ナレッジキャピタル7階
（大阪市北区大深町3番1号）
　
◆参加費：1,000円　

◆定　員：20名
　
◆持ち物：筆記用具、問題用紙とご自身の解答（過去問を扱う場合）、電卓（事例Ⅳの場合）　

◆開催日時・内容
※内容や扱う事例は変更となる場合があります。
下記が最新の予定となります。

10月7日（火）19:00～21:30　平成23年度試験（事例Ⅲ）実施と添削指導
10月10日（金）19:00～21:30 平成23年度試験（事例Ⅳ）実施と添削指導

お申込みはこちらから