[1次2次] 理系のための診断士学習法(#2:微分の公式)
中小企業診断士を目指す皆様、おはようございます。がんちゃん/岩間です。
診断士試験の学習過程では、色々な数式や数学的概念が出てきます。先週に引き続き、今週も、診断士試験向けテキストや予備校の講義では省略される内容を見てみます。今回は、経済学で出てくる微分の公式(![]() →
→![]() )を扱います。
)を扱います。
(先週の内容:DCF法の公式、コブ・ダグラス型生産関数の成長方程式/全要素生産性(TFP) )
今回は、「なぜ![]() を微分すると
を微分すると![]() になるの?」という疑問に、直感的に説明し、合わせて厳密な説明もします。
になるの?」という疑問に、直感的に説明し、合わせて厳密な説明もします。
試験対策としては、公式の意味を押さえる必要はありませんが、別の角度から見てみると理解が深まるかもしれません。本記事は、せっかくだから一歩踏み込んで知っておきたいという方にお読みいただければと思います。(また、ちょっとした頭の体操にもなるかもしれません)
◆目次
- 4.[経済] 微分の公式
- 微分に関して押さえておくべきこと(診断士試験の範囲)
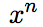 を微分すると、なぜ
を微分すると、なぜ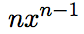 になるのか?
になるのか?
- (1)直観的な説明
- (2)きちんとした説明
- (3)きちんとした説明(裏技)
◆微分に関して押さえておくべきこと(診断士試験の範囲)
まずは、診断士試験の範囲として押さえておくべきポイントを見てみます。
|
【微分に関して押さえておくべきポイント(診断士試験の範囲)】
※それぞれの読み方は「ワイプライム」と「ディーワイディーエックス」です。 |
具体例で見てみます。まずは、微分係数の正負による、関数やグラフの特徴を見てみます。
| 微分係数の値 | 関数はどのような状態か | グラフの特徴 | |
|---|---|---|---|
| + | 増えている | 右上がり | 接線の傾き(の値)が+ |
| 0 | 増えても減ってもいない | (局所的に)平坦 | 接線の傾き(の値)が0 |
| - | 減っている | 右下がり | 接線の傾き(の値)が- |
続いて、微分係数の大小による、関数やグラフの特徴を見てみます。
| 微分係数の値 | 関数はどのような状態か | グラフの特徴 | |
|---|---|---|---|
| -2 | 急激に減っている | 右下がり(急) | 接線の傾き(の値)が約-63度 |
| -1 | 緩やかに減っている | 右下がり(緩やか) | 接線の傾き(の値)が-45度 |
| 1 | 緩やかに増えている | 右上がり(緩やか) | 接線の傾き(の値)が45度 |
| 2 | 急激に増えている | 右上がり(急) | 接線の傾き(の値)が約63度 |
◆本題: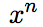 を微分するとなぜ
を微分するとなぜ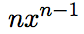 になるのか?
になるのか?
【1.直感的な説明】
これから、微分の意味合いを考えながら、この公式を導いてみます。(![]() 、
、![]() の順に見た後、最後に一般的な
の順に見た後、最後に一般的な![]() の場合を見てみます)
の場合を見てみます)
まずは![]() の場合です。
の場合です。
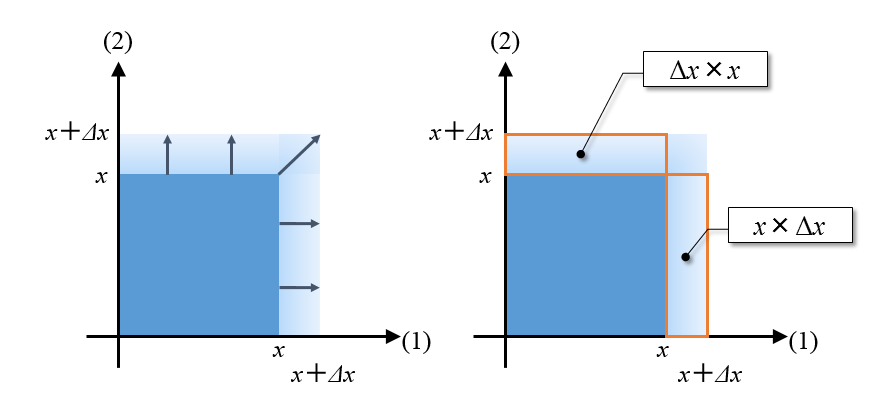
微分は「xが増えたら、全体(![]() )がどれだけ増えるか」を考えるものでした。そこで、「xがΔxだけ増えてx+Δxとなった」と想定して、「xのとき」と、「x+Δxのとき」を比較します。
)がどれだけ増えるか」を考えるものでした。そこで、「xがΔxだけ増えてx+Δxとなった」と想定して、「xのとき」と、「x+Δxのとき」を比較します。
図1の左のグラフには、![]() と
と![]() の両方を図示しています。小さい正方形(濃い部分)の面積が
の両方を図示しています。小さい正方形(濃い部分)の面積が![]() で、大きい正方形(濃い部分+薄い部分)の面積が
で、大きい正方形(濃い部分+薄い部分)の面積が![]() です。
です。
このとき、増えた分は、L字型の薄い部分の面積です。この大きさは、およそ(※)、図1の右のグラフの2箇所の赤枠内の部分と等しいです。
赤枠1個分の面積はxΔxなので、増加分全体の面積は 2xΔx です。
(※「およそ」と書いた理由は、後述します)
これに基づいて、微分係数(=増加分÷Δx)を求めると、2xとなります。
次に![]() の場合です。
の場合です。
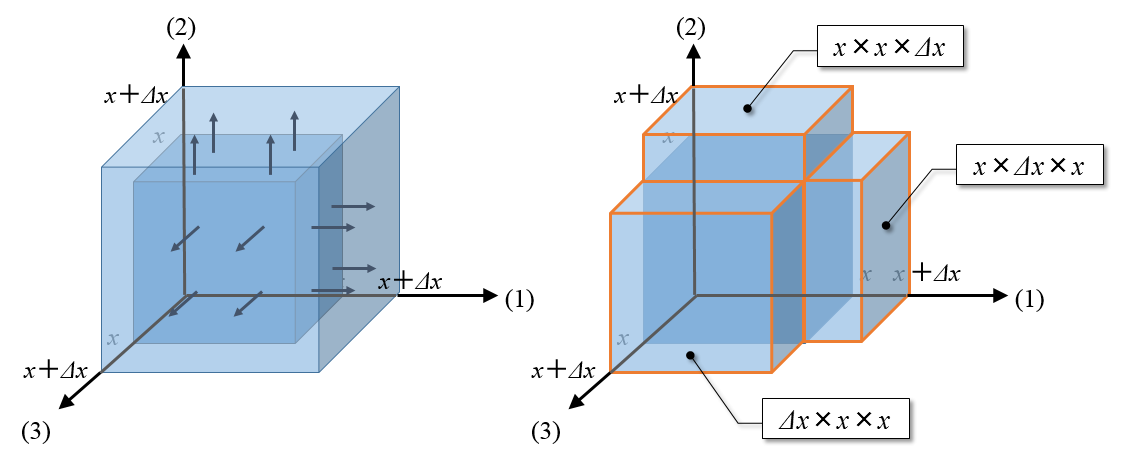
先ほどと同様に、「xのとき」と、少し増えた「x+Δxのとき」を比較します。
![]() と、
と、![]() を図で表してみます(図2左)。小さい立方体(濃い部分)の体積が
を図で表してみます(図2左)。小さい立方体(濃い部分)の体積が![]() 、大きい立方体(薄い部分)の体積が
、大きい立方体(薄い部分)の体積が![]() です。
です。
このとき、増えた分は、およそ、図2の右のグラフの3か所の赤枠内の部分と等しいです。
赤枠1個分の体積は![]() なので、増加分全体の体積は
なので、増加分全体の体積は![]() です。
です。
これに基づいて、微分係数(増加分÷Δx)を求めると、![]() となります。
となります。
最後に、一般的な場合(![]() )です。人が図で認識できるのは3次元までなので、ここからは図を用いずに考えます。
)です。人が図で認識できるのは3次元までなので、ここからは図を用いずに考えます。
- これまで同様、「xのとき」と、少し増えた「x+Δxのとき」を比較します。
- 増分は、これまでの赤枠部分と同様に、およそ、いくつかの合同な部分に分けることができます。
- その個数は、軸の個数と同数のn個です。
- 1個分の面積・体積(※)は、
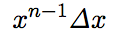 です。
です。
(これは、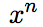 =x×x×…×x(xをn回掛ける)のうち、軸方向の1個のxを、Δxに置き換えたものになります)
=x×x×…×x(xをn回掛ける)のうち、軸方向の1個のxを、Δxに置き換えたものになります)
- 従って、増加分全体の面積・体積(※)は、
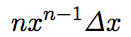 です。
です。 - これにより、微分係数(増加分÷Δx)は
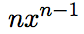 となります。
となります。
※これを一般に「n次元超体積」と呼びます。面積は2次元超体積で、体積は3次元超体積です。
最後に、公式![]() を見てみると、
を見てみると、
- 最初のnは、「軸の数nだけ、小さい部分(赤枠部分)があるから」
- xの右上のn-1 は、「
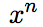 のうち、軸の1個分に相当するxを、Δxに置き換えたから」となります。
のうち、軸の1個分に相当するxを、Δxに置き換えたから」となります。
なお、これまでで「およそ」と表記した箇所について補足します。![]() 、
、![]() 、
、![]() それぞれについて、増加分を、合同な要素(赤枠部分)に分けましたが、その時に漏れている箇所があります(
それぞれについて、増加分を、合同な要素(赤枠部分)に分けましたが、その時に漏れている箇所があります(![]() のときは、右上にある小さな正方形です。
のときは、右上にある小さな正方形です。![]() のときは、細長い角柱3個と、小さい立方体1個です)。これらの部分の面積・体積は、次の理由から0と見なせます。
のときは、細長い角柱3個と、小さい立方体1個です)。これらの部分の面積・体積は、次の理由から0と見なせます。
- これらの部分の面積・体積は、Δxの2乗以上の和で表されます。(
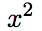 のときは
のときは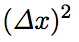 、
、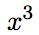 のときは、
のときは、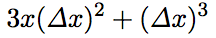 です)
です) - そのため、これらの部分は、微分係数を増加分÷Δxとして求めた際にも、1次以上のΔxが残ります。
- 最終的に、Δxを微小部分として0に近づける(極限を取る)ため、残った部分は0になります(0に収束すると言います)。
【2.きちんとした説明】
(本項は、数学的に高度な内容を含みますので、読み飛ばしていただいて構いません)
1では直観的に公式を見てみました。ここでは、数式上で少し厳密に見てみます。
次のように導けます。
それぞれの式変形の意味は次のとおりです。
- (1)→(2):「x+Δxのn乗」の部分を、2項定理を用いて展開する。併せて、分母を計算する(xが消える)。
- (2)→(3):分子を計算する(xのn乗の項が消える)。
- (3)→(4):分子の各項を、分母のΔxで割る。
- (4)→(5):Δxを含む項を、0にする。
- (5)→(6):係数の部分を、nで表す。(係数の部分は「n個の要素から1個を選ぶ組み合わせの数」を表します。)
【3.きちんとした説明(裏技)】
(本項は、数学的に高度な内容を含みますので、読み飛ばしていただいて構いません)
2で行った説明は、数式上で厳密に、定義に則って行ったものでした。一方で、微分に関する別の公式を使うと、次のように説明することができます。(この方法は、対数微分法と呼ばれます。前回の記事で紹介した、![]() を使います。)
を使います。)
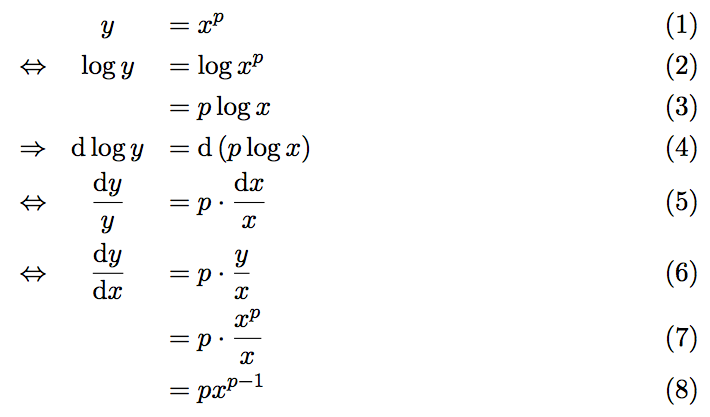
それぞれの式変形の意味は次のとおりです。
- (1)→(2):両辺の対数をとる(両辺にlogを付ける)
- (3)→(4):微分形式で表記する
- (4)→(5):
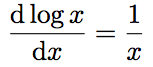 という式を用いて、両辺を変形する
という式を用いて、両辺を変形する - (5)→(6):両辺にyを掛け、dxで割る(左辺にdy/dxを持ってくるため)
- (6)→(7):xのp乗の部分に、(1)の式を代入する。
年末が近づいてきており、忙しく過ごしていることと思います。年末はいろいろとやるべきことが多かったり、ダラダラ過ごしがちだったりします。来年に1次試験・2次試験を受験される方は、診断士試験向けの学習が後回しにならないよう、計画を立てて進めていただくことをお勧めします。
以上、がんちゃん/岩間でした。
====================
皆様の応援がタキプロの原動力となります。
ぽちっと押して、応援お願いします♪
====================