経済学・ゲーム理論 by かわけん

皆さん、こんにちは。
「人と会社を健康で幸せにする」、体と心と会社の医士（医師＋中小企業診断士）のかわけんです。
自分の専門である、医療、労働衛生、メンタルヘルスの分野から皆様に役立つ情報を発信したいと考えています。特に、私と同じような方（高齢、独学、初学者）の助けになれば幸いです。よろしくお願いします。

2次試験が終わり１ヶ月ほど経ちましたね。皆さん、いかがお過ごしでしょうか。
先日、タキプロ主催の「2次筆記試験お疲れ様セミナー」に参加し、受験生の方と話させていただきました。事例Ⅳが相当難しかったらしいですね。私もちらっと問題を見ましたが、もう全然解けませんでした。本当に一年の時の流れは早いものです。

受験生の皆さんは結果を心配されていましたが、今はあまり悩む必要はないと思います。私も事例Ⅳで絶望感を味わったのですが、結果的に合格でした。皆ができないときは、かなりの下駄が履かされていると聞きます。タキプロの仲間の話を聞いていても、2次試験の終了後に合格を確信できるような方は本当に少数で、大多数の人はだめだと思いながら結果的に合格となっています。今は過度に悩まず、結果を待ちましょう。年明けに、吉報が来るといいですね。
また、今後どうやって事例Ⅳを勉強すればいいのか悩まれておられる方がけっこうおられました。そのような方には、私の恨みのこもった長文ブログ、「令和二年の事例Ⅳ、どうすべきだった？　かわけんの経験より分析してみた！」をお読みください。何か参考になることがあると思います。

そして、今年残念ながら2次試験に進めなかった方、出題された問題を検討しましたか？
2次試験を受けた方がのんびりしておられる今が差別化のチャンスです。このスキに頑張って勉強して、来年は受験生の立場で2次試験を迎えましましょう。今年2次試験を受けた方の大多数は来年も2次試験を受けます。 そのライバルに負けないようにしてくださいね。

さて今回、いただいたテーマは経済学です。
正直、経済学はズブの素人です。もともと理系の人間なので、診断士試験までは経済学を勉強したことは全くありませんでした。最初に勉強を始めるときはとても困りましたが、以前のブログで投稿したようにマンガや副読本で基礎を固め、その後スピードテキストをやりました。ある程度知識が身につくと、グラフを使っていろいろな事象を解析する経済学はなかなか面白かったです。
ただ、所詮はなんとか試験をクリアしたズブの素人であることには変わりません。

今回、経済学の中で何をテーマとして取り上げるかは随分悩みました。
ただ、もうタキプロ活動も終盤に差し掛かっており、私が勉強の話を書くのは今回の経済学が最後です。すなわち経済学を含む診断士の勉強をする機会は、今後もうないかもしれません。
そこで最後の機会を満喫すべく、以前から勉強したかったゲーム理論をテーマとして取り上げることにしました。 今までのタキプロのブログを調べてみましたが、ゲーム理論を詳しく取り上げられたブログはなかったのでちょうどいいのではないかと思ってます。

ところで先日タキプロのセミナーで、私のブログを読んでいると言われる受験生の方に初めて会いました。本当に初めてだったので、ちょっと嬉しかったです(T_T)。
そのような方々の期待に応えられるように今回も長い文章を投稿します。ブログは気軽にサクッと読みたいと思われる方には申し訳ありません。長いのはイヤと言われる方は、受験生は試験向けの前半を、診断士の方はちょっと面白めに書いた後半だけでも読んでいってください。
それから表をたくさん挿入したため、かなり小さくなりました。見にくくなって、本当にすみません。上手に拡大して見てください。
皆さんに、私のブログが役立てば幸いです。よろしくお願いします。

私は今まで以下のような投稿をしています。興味のある方はご覧ください。
※どれも長いですm(_ _)m
１回目　　合格体験記
２回目　　令和二年の事例Ⅳ、どうすべきだった？　かわけんの経験より分析してみた！
３回目　　ITを活用した効率良い勉強方法 by かわけん
４回目　　運営管理の勉強で使った副読本 by かわけん
５回目　　まだ1次試験に間に合います。気合を入れて最後のラストスパート！ by かわけん
６回目　　事例１・幸の日も毛深いネコとモチベーション by かわけん
７回目　　独学・初学者のための2次試験の解き方 by かわけん
８回目　　インターネットから学んだ事例Ⅲのエッセンス
９回目　　審査員から皆さんに伝えたいこと by かわけん
１０回目　事例Ⅱの戦略とモデル企業 by かわけん

■はじめに

ゲーム理論って名前がとても魅力的ですよね。だって習得したらなんかうまく相手に勝てそうな気がしませんか。
飼い主を無視するウチのネコから好かれたり、嫁さんをうまいこと言いくるめてお小遣いをいただいたり、できそうな気がしますよね。
以前から、とても面白そうじゃないかなと前から思っていました。

さてそのゲーム理論ですが、1次試験には結構高い頻度で出題されています。ここ5年で3回ですね。試験ではパターンさえ覚えれば解きやすいので、比較的対応しやすい問題だと思います。
私が試験で使ったスピードテキスト４経済学・経済政策では、不完全競争の寡占市場の中に出てきます。

寡占市場に参加する企業のように、相手の行動を考慮した上で自らの意思決定を行うことがある。このような戦略的行動は、企業のみならずさまざまなところに存在する。ゲーム理論とは、互いに影響を与え合うプレイヤーによる意思決定に関する理論である。

スピードテキスト４経済学・経済政策

と書かれています。
他に勉強に使った本でも、ゲーム理論は「寡占市場において各企業はどのような行動を取るのか」を説明するときに用いられてました。そんなことから、私も受験生時代は寡占市場の理論と考えていました。でももし、寡占市場における意思決定なら、飼いネコから好かれたり、嫁さんからお小遣いをもらったりするのはとても無理ですよね。

ただなんとなく寡占市場に限られるものではないんじゃないかとも感じていました。そして昔から興味のあったフォン・ノイマンが絡んでいることもあって、ちょっと本格的に勉強したかったので、この機会を活かしがっつり３週間ほどやってみた次第です。
そうするとゲーム理論は、経済学の中で実に広い範囲で用いられているとても有用な理論であることがわかりました。また日常生活でも十分に役に立ちそうな理論であると感じました。

今日はその中からエッセンスを面白くお話しします。このブログを通じてゲーム理論の一部でも習得いただければ嬉しいです。
タキプロブログなのでもちろん受験生向けの内容も入れています。ただ本当に基礎から説明するものではありません。ちょっと知っている方向けです。
また、今回のブログに記載するまとめは、あくまでも経済学は素人のかわけんが本の知識とネット情報を元に考えた私見です。参考にされる時は十分にご注意ください。
それからブログを書くのに使用したのは以下の書籍です。たくさん並んでいますが、全てを最初から最後まで読んだわけではありません。相変わらずマンガが入っていますがご容赦ください。

• マンガでわかるゲームの理論（ポーポー・ボロダクション著、SBクリエイテイブ）
• マンガでやさしくわかるゲーム理論（川西諭著、日本能率協会マネジメントセンター）
• ゲーム理論と情報の経済学（神戸伸輔著、株式会社日本評論社）
• ゲーム理論入門（天谷研一著、日本能率協会マネジメントセンター）
• 現在経済学（瀧澤弘和、中公新書）
• 囚人のジレンマーフォン・ノイマンとゲームの理論（ウィリアムパウンドストーン著、青土社）
• 最後通牒ゲームの謎（小林桂世子著、日本評論社）
• 大学4年間の経済学が10時間でざっと学べる（井堀利宏著、角川文庫）
• 医療現場の行動経済学（大竹文雄著、東洋経済新報社）
• 世界標準の経営理論（入山章栄著、ダイヤモンド社）

１ゲーム理論の基礎

まずはゲーム理論の基礎です。

そもそも、社会の中で人間は意思を持って行動しています。そして現在社会ではビジネスを含め、人間が社会で生活するおよそあらゆる場面に駆け引きが存在するため、意思を持って行動する際に望むと望まざるとにかかわらず様々な駆け引きに、参加しているといえます。そのような駆け引きに参加している状況、「自分の利得が相手の行動に依存し、相手の利得が自分の構造に依存している時（複数の意思決定者間の相互依存関係）」はゲームの状況と言われています。
そして「ゲームの状況（複数の意思決定者間の相互依存関係）を分析する理論」がゲーム理論と定義されています。すなわち簡単に言うと、ゲーム理論は社会の中で行動する人間の駆け引きを考えるための理論です。

ここでゲーム理論と対比されるのは、最適意思決定あるいは市場均衡です。われわれが行う意思決定が、すべてゲーム的状況での意思決定というわけではなく、ゲーム以外での意思決定が２種類あります。１つは、統計的問題や技術的問題を解くことです。たとえば、外出する際に傘を持っていこうかとか、どういう形の車が一番速く走るかという問題です。これらは、相手がいない状況での最適化なので相互依存関係にはなりません。もう１つは、市場での消費と生産の決定です。完全競争市場では、「価格」が市場で決定し、市場の参加者は行動を決定すると仮定されるので、相互依存関係にはなりません。すなわち、この２つの意思決定はゲーム理論の対象ではありません。言い換えれば、これ以外の意思決定はすべてゲーム理論が適応される可能性があります。

目的
ゲーム理論を学ぶと以下のことに役立つとされています。
・冷静によりよい選択が取れるようになる
・視野を広げ新しいものの見方を獲得できる
・知識や直感の裏付けになる
・相手に望ましい行動を取らせるために、ゲームのルールを策定できるようになる
これらを見ると、ゲーム理論は単に寡占市場を分析するだけではなく、実社会でもとても役に立ちそうな理論であることがわかります。

前提条件
ゲーム理論には前提条件があります。それが以下の２つです。
・プレイヤーは常に「ルールに従って合理的に行動する」
・合理的な行動とは、「自分にとって最も大きな利得を得られる行動」を意味する

構成要素
ゲームの構成要素は「プレイヤー」「戦略」「利得」の3つです。
・プレイヤー：意思決定を行う主体
・戦略：相手がこうしてきたら自分はこうするというような、状況に応じた自分の行動の計画
・利得：効用や利潤のように目的となる指標すべて
構成要素の３つを表にしたものが利得表になります。

ゲーム的状況
そのゲーム的状況は、以下のような観点から分類されます。
・協力の有無：協力ゲーム・非協力ゲーム。非協力ゲームの典型は2人ゼロサムゲーム
・情報の共有の有無：情報完備ゲーム・情報不完備ゲーム
・意思決定の回数：単期間ゲーム・複数期間ゲーム
・意思決定の手順：同時手順ゲーム・交互手順ゲーム

すなわち、ゲーム理論は、前提条件、構成要素、ゲーム的状況の分類から、合理的な行動を分析する理論であると言えます。

その分析結果は、「プレーヤーがどの戦略を選ぶのか」という理論的予測である解で表されます。ゲーム理論における代表的な解には、ナッシュ均衡、ベイズ均衡、完全ベイズ均衡、分離均衡、一括均衡などがあります。
解に関するものは以下のようなものがあります。
・最適反応：自分の利得が最も大きくなる戦略
・支配戦略：相手がどの戦略をとっても、自分が常にとるべき最適反応の戦略
・支配戦略均衡：互いに支配戦略となっている組合せ。常に存在するとは限らない。複数成立することはない。ナッシュ均衡の特殊型。
・ナッシュ均衡：互いに最適な戦略を選択している状態。ゲーム理論では通常ナッシュ均衡を使った分析を行う。常に存在するとは限らない。複数成立することがある。支配戦略均衡は必ずナッシュ均衡だが、ナッシュ均衡が必ずしも支配戦略均衡ではない。ナッシュ均衡が実現されると、ゲームは安定状態に入る。複数のナッシュ均衡がある場合、プレイヤーがどれを選ぶのかは、論理的に説明はできない。
・パレート改善：誰からも文句が出ず、得をする人が１人はいる変化
・パレート非効率：パレート改善が可能な状態
・パレート効率（最適）：他の誰かの利益を悪化させない限り、どの人の利益も改善することができない状態。言い換えれば、パレート改善できない状態
・囚人のジレンマ：両者にとって高い利益を得ることが可能であるのに、支配戦略の結果、低い利益しか得られない状態。ナッシュ均衡とパレート効率が一致しない状態。これは合理的な行動が必ずしも最善の選択ではないことを示している。

ゲーム理論の解に関する説明を列挙しました。
問題はゲーム理論の「解」は真理なのかということです。これに関して、導き出された「解」は「絶対的な真理」というわけではなく、「人間が合理的だと仮定した場合の、理論から予測される合理的な行動」とされています。

ゲーム理論の習得
今回の目的であるゲーム理論の習得には、３段階あるとされています。
Step 1 モデルの理解：構成要素とゲーム的状況を観察し、モデルを理解できるようになる
Step 2 解を解釈：モデルを理解して、ゲーム理論でプレイヤーがどのような意思決定や行動を選択するが分析して「解」を得る
Step 3 実際の状況にゲーム理論を適用：自分が直面する現実の状況に対して、モデルの理解、解の解釈を行い、自分のすべき行動の判断を行う

上記のStepを完了して「ゲーム理論を習得した」といえるようになります。
今日のブログでは３Stepでのゲーム理論習得を目指したいと思います。

２令和2年度1次試験　経済学・経済政策　第22問

それでは例題として、我々１２期が受験したときに出題された経済学・経済政策の第22問を検討しましょう。
ゲーム理論の基本的な解き方も説明していきます。

問題
夫婦による家事分担は重要である。会社員の太郎さんと主婦の花子さんには、夕方の家事に関して「協力する」「相手に任せる」という選択肢がある。 ー中略ー。下表は、以上の説明を、利得マトリックスにまとめたものである。マトリックスの左側が太郎さんの利得、右側が花子さんの利得である。

令和2年度1次試験　経済学・経済政策　第22問

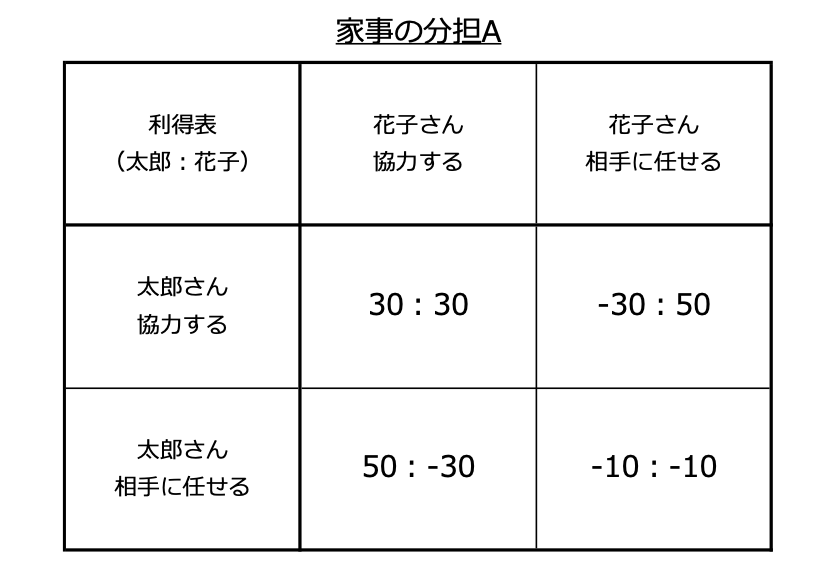
まずは、Step 1 モデルの理解です。基本的な分析は以下のとおりです。

ゲームの構成要素
・プレイヤー：太郎さん、花子さん
・戦略：「協力する」と「相手に任せる」
・利得：利得表（家事の分担A）
ゲーム的状況：非協力、情報完備、短期間、同時手順

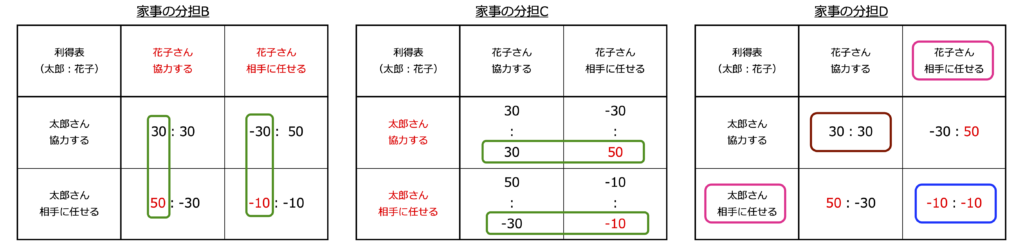
次はStep 2 解を解釈を行います。個々の取るべき戦略を検討します。まずは太郎さんです（家事の分担B）。
１花子さんの連略を協力するに固定します（家事の分担Bの左の緑枠）。太郎さんの戦略は50の相手に任せるになります。
２花子さんの連略を相手に任せるに固定します（家事の分担Bの右の緑枠）。太郎さんの戦略は-10の相手に任せるになります。

次は花子さんの取るべき戦略を検討します（家事の分担C）
３太郎さんの連略を協力するに固定します（家事の分担Cの上の緑枠）。花子さんの戦略は50の相手に任せるになります。
４太郎さんの連略を相手に任せるに固定します（家事の分担Cの下の緑枠）。花子さんの戦略は-10の相手に任せるになります。

最後に解を検討します（家事の分担D）
赤字の部分を選択します。太郎さんの支配戦略は相手に任せる（家事の分担Dのピンク枠）、花子さんの支配戦略は相手に任せる（家事の分担Dのピンク枠）となり、赤文字のそろう右下がナッシュ均衡、ピンク枠のそろう右下が支配戦略均衡（家事の分担Dの青枠）、左上がパレート効率（家事の分担Dの茶枠）になります。
この設問では、ナッシュ均衡とパレート効率が一致しませんから、囚人のジレンマの状態です。

これが基本的な考え方です。
次に少しづつ利得を変更して条件を変えました。変更した数字にはアンダーラインを引いてます。各々の状態を示します。

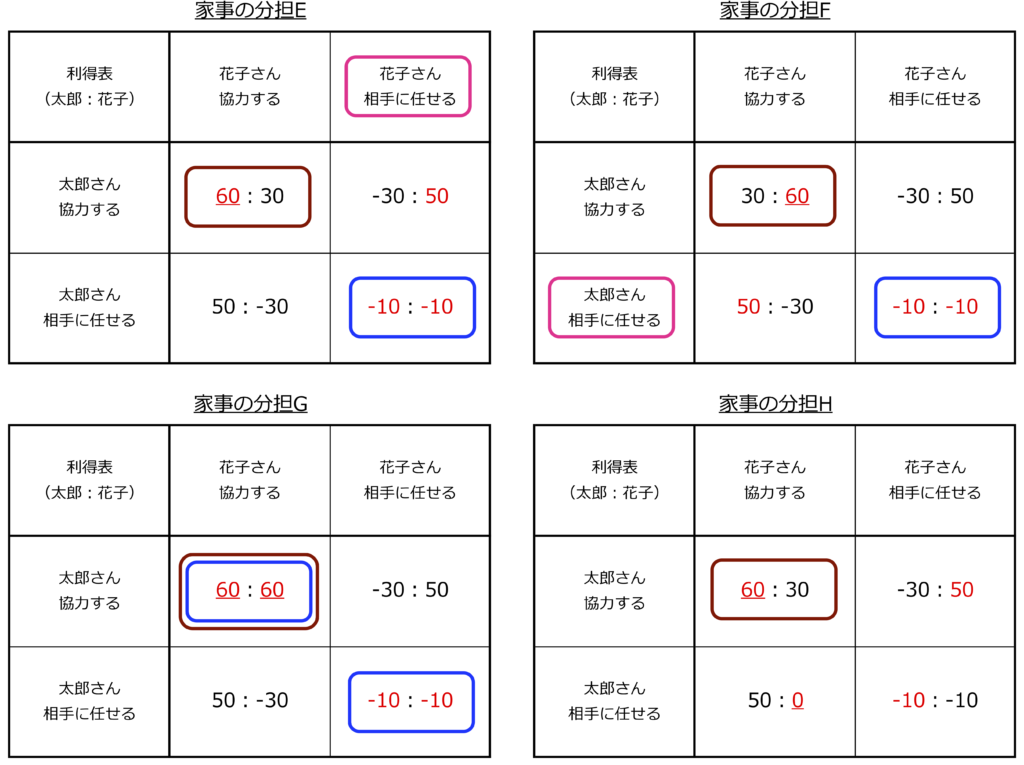
• 家事の分担E：太郎さんの支配戦略がありません
• 家事の分担F：花子さんの支配戦略がありません
• 家事の分担G：どちらも支配戦略がありません
• 家事の分担H：支配戦略もナッシュ均衡もありません

いずれもパレート効率はお互い協力するになっています。

以上のようになるのがゲーム理論の基本的な考え方です。これだけ知っておけば、1次試験には対応可能だと思います。
※分析は自分で行った上、ネット上の戦略形非協力２人ゲームのナッシュ均衡とパレート最適解析プログラムで検算を行いました。

３ゲーム理論と経済学ー寡占市場の理論？ー

さて次はゲーム理論の背景を考えます。
診断士試験のテキストや経済学の初歩的な本では、ゲーム理論は不完全競争の寡占市場のところで出てきます。ただ「本当に寡占市場なの？」という気がしていたので、今回勉強をしたわけです。

試験勉強を終えた我々の理解によると、経済学はマクロ経済学とミクロ経済学があります。そして、システムの構成要素からシステム全体へという方向性を持つ説明と予測を行う学問は「要素還元主義」と呼ばれ、通常はミクロ経済学と呼ばれています。そのシステムの構成要素の行動は、意思決定者の意思決定によって行われます。すなわちミクロ経済学は構成要素の意思決定の上に成り立っています。その意思決定は合理的に行われるというのが経済学の大前提になっています。

伝統的な経済学では、市場メカニズムの分析を通して、各人が自己利益のみを考えて合理的に行動すれば、社会的に望ましい結果が得られるという、アダム・スミスの「見えざる手」という概念を重視していました。診断士試験の受験生はご存知の、完全競争市場（前提として、全員プライステイカー、売り手と買い手が多数、完全情報、特別の選好なし）において、供給曲線と需要曲線が一致する点が市場均衡で、交点が価格と量を決定するグラフですね。そしてその調整は、「見えざる手」が行っており、市場均衡は社会のメリット（社会的総余剰）が最大になるというものです。
しかし実際の社会、特に寡占市場など意思決定者間の相互依存関係のある場合、談合・カルテルや値下げ競争という「見えざる手」とういう市場メカニズムの理論だけでは説明しきれない現象がありました。

そこで数学者のジョン・フォン・ノイマンと経済学者のオスカー・モルゲンシュテルンが、その原因は人々の間の駆け引きにあると考え、複数主体が関わる意思決定の問題や行動の相互依存的状況を数学的なモデルを用いて研究する理論を考え、1944年に『ゲームの理論と経済行動』 としてまとめ出版しました。そのとき、一人の意思決定者の意思決定を研究する「意思決定理論」に対して、複数の意思決定主体が絡んだ意思決定の状況で何が選択されるのかを研究する「ゲーム理論」が誕生したことになります。
その後、ゲーム理論はその有用性からどんどん適応が拡張され、とても広い範囲で用いられるようになりました。Wikipediaのゲーム理論の項には、以下のように記載されています。

ゲーム理論の対象はあらゆる戦略的状況。「戦略的状況」とは自分の利得が自分の行動の他、他者の行動にも依存する状況を意味し、経済学で扱う状況の中でも完全競争市場や独占市場を除くほとんどすべてはこれに該当する。
さらにこの戦略的状況は経済学だけでなく経営学、政治学、法学、社会学、人類学、心理学、生物学、工学、コンピュータ科学などのさまざまな学問分野にも見られるため、ゲーム理論はこれらにも応用されている。

Wikipedia

今日の経済では、独占企業は国家政策でほぼ成立せず、完全競争市場の条件が成立しない状況が多くなっているため、ゲーム理論の成立する寡占市場が成立しやすくなっています。そこで、現代の経済を理解する上では、ゲーム理論と情報の経済学は市場分析と並んで不可欠な知識となってきています。

また、現在経済学（瀧澤弘和著　中公新書）には以下のように記載があります。

ゲーム理論は、それまでの経済学がほとんどの場合に、市場を経由した主体間の相互作用に焦点を当ててきたのに対して、プレーヤーの行動が直接的に他のプレーヤーに影響を与えあう「ゲーム的状況」の経済分析へと経済学を拡張するものであった。これにより、私益の追求が社会全体の利益に一致する「見えざる手」の論理が働く市場の世界とは異質の世界を分析の俎上に載せることになった。
ゲーム理論が経済学に与えた甚大な影響は数々あるが、特に強調したのは、ゲーム理論によって、人間行動の観察された規則性を説明する際に、信念と行為の組合わせという観点が導入されたことである。その結果として、われわれは異なる複数の均衡が存在しうることを理解できるようになった。

広範囲の経済的状況を定式化できるゲーム理論の表現力は、市場に限定されない取引制度の分析を可能にした。

ゲーム理論それ自体は、数学的に定式化された抽象的なゲームを対象として、そこにおける人間の行動選択の仕方を理論的に予測するための均衡概念を提案するものである。

現在経済学（瀧澤弘和著　中公新書）

これをみると、市場に限定されない取引から人間の行動選択まで適当が広がっており、ゲーム理論が経済学に与えた影響がいかに大きかったかがよくわかります。
加えて、以下のような記載もあります。

経済学ディシプリンの様々な経営理論を解説してきた。近代経済学では、実はこれらの理論ほぼすべての背後に、「ゲーム理論」の存在がある。ゲーム理論はそれ自体一つの理論でもあるが、同時に経済学では一種の「数理的な言語ツール」になっており、この言語ツールを通じて様々な経済・ビジネス事象が記述されている

世界標準の経営理論（入山章栄著、ダイヤモンド社）

この本によるとゲーム理論は、近代経済学の理論ほぼすべての背後に用いられる言語ツールとされているようです。ノーベル経済学賞でもゲーム理論関連のものが多数あると書かれていました。
すなわち、ゲーム理論とは受験参考書に出ている単に不完全競争下の寡占市場に適応される理論というだけでなく、現在の社会の広い範囲で適応される理論であると考えられています。

４ゲーム理論の実際への適応・かわけん起業編

さてここまででゲーム理論の基礎、モデル化、解の考え方、経済学との関連についてお話してきました。
ここからはStep 3 実際の状況にゲーム理論を適用について検討したいと思います。かわけんの事例です。

かわけんは2021年7月から京都大学の医療ヘルスケア・イノベーション起業家人材育成プログラム（HiDEP）に参加していました。そのHiDEPのプログラムで、いいプロジェクトができたので起業することを考えました。
かわけんの計画では、100初期投資して、10働いて、20の利益が予定されています。一生懸命働けばその２倍位は利益が出そうです。
かわけんは中小企業診断士なので、５−１０年で初期投資を取り戻せると事業計画をたてました（診断士らしからぬザツイ事業計画とか突っ込むのは止めてくださいね、笑）。

ただ１人で起業するのはとても不安です。そこでHiDEPのメンターに起業するかも含めて相談しました。
メンターは、「かわけん君、起業は不安だね。だから、一緒にやってくれる仲間を誘いなさい。ただ、誘われたほうも不安になるから、仲間に初期投資は求めないでね。また利益が均等に分けたほうがいいよ。」とアドバイスをくれました。

かわけんはメンターの意見に賛成し仲間を誘うことにしました。もちろん投資はなしで、利益は均等に分けます。かわけんは仲間がそこまで働いてくれることは期待していません。半分ぐらい働いてくれれば充分、自分と同じはたらぐらい働いてくれればとても満足、と考えています。
ところでかわけんは最近ゲーム理論を覚えたので、どう行動すればいいかゲーム理論で考えることにしました。
　

ルール
・100の初期投資はかわけん負担
・10働くと20の利益なる（比例関数）
・利益はかわけんと仲間で均等割

ゲームの構成要素
・プレイヤー：かわけん、仲間
・戦略：かわけんは「不参加」「参加・普通に働く」「参加・一生懸命に働く」。仲間は「不参加」「参加・かわけんの半分働く」「参加・かわけんのなみに働く」
・利得：利得表１

ゲーム的状況：非協力、情報完備、短期間、同時手順
以上のような設定です。Step 1 モデルの理解はできましたね。
　

次は条件を変えながらStep 2 解を解釈を行います。
まず簡単な利得表を書いてみました（表１）。

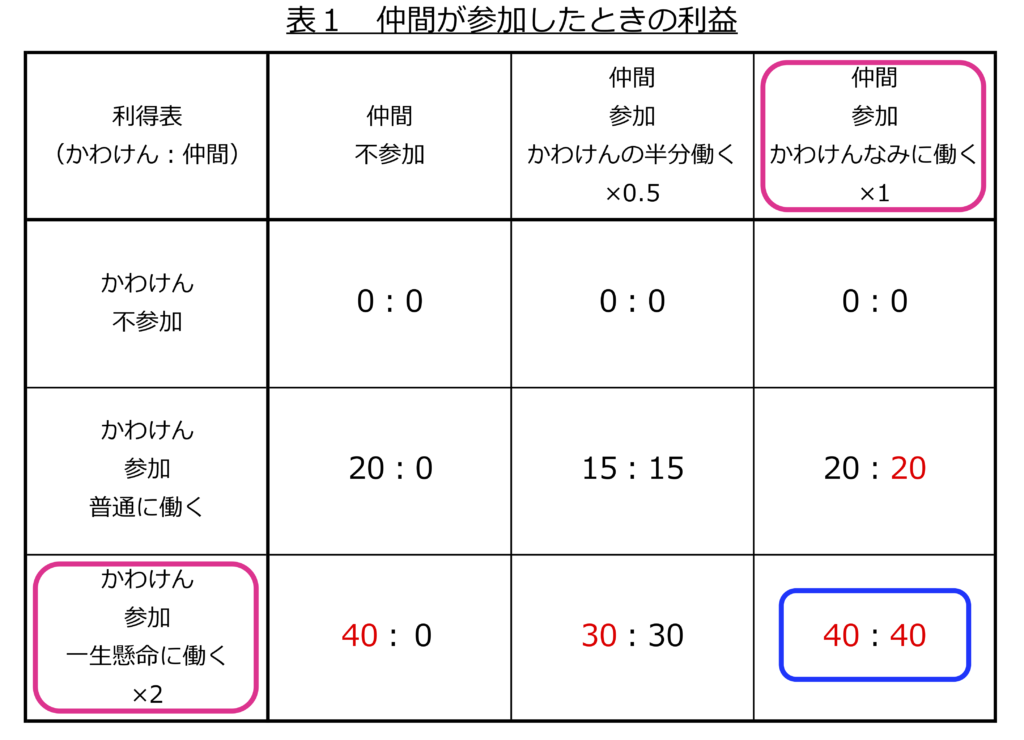
2人でがんばって働くと利益がぐっと増えるようです。どちらも支配戦略は一生懸命働くと言うことになり、ナッシュ均衡、支配戦略均衡になりました。かわけんはとても素晴らしいと、アドバイスしてくれたメンターに感謝しました。
でもちょっと考えました。「かわけんのほうがよく働いているのに利益は均等だよな。これは平等かな？働いてる量はどうなんだろう?」

そこで労働量を計算してみました（表２）。

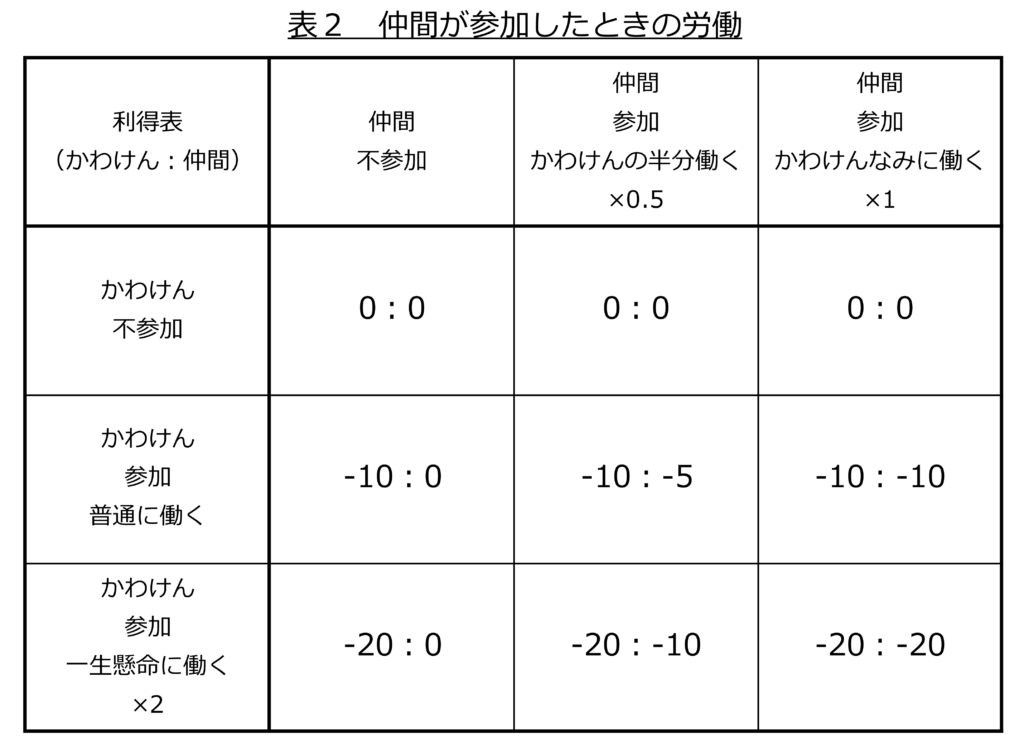
利益と労働の関係を考えるために、先程の利益と労働の表を素直に足すことにしました。合算すると真の利益がわかるんじゃないかと考えました。

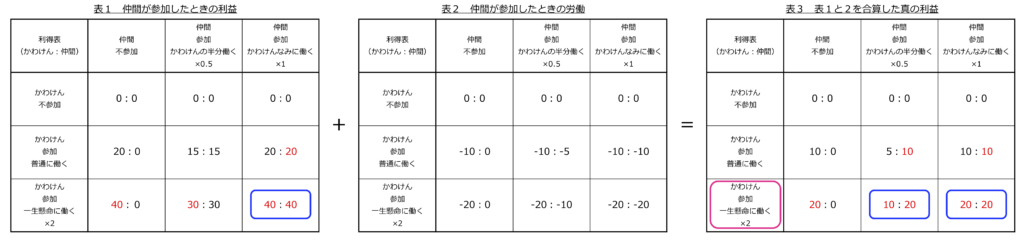
かわけんの支配戦略は一生懸命働くになりました。仲間の支配戦略はありません。ナッシュ均衡は2つあります。かわけんは自分の利益が少ないのが気になりました。また仲間の働き方によって自分の利益が減っているのが気になりました。

そこでもし働き方がこのままで利益が半分になったらどうなるんだろうと計算してみることにしました（表４と５）。

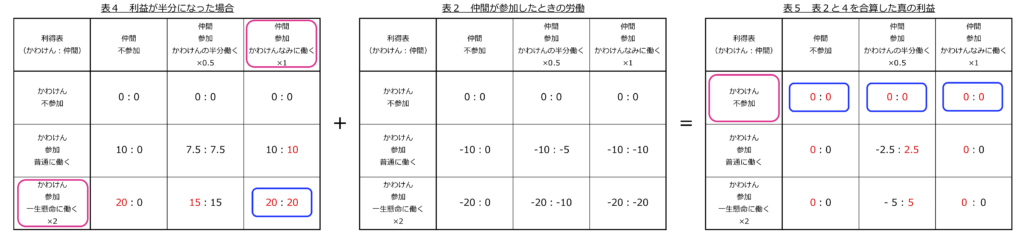
単純に利益だけを見るとどちらも一生懸命働くことが支配戦略になっています（表４）。ただし労働を加味した真の利益を計算してみると、かわけんの利益はすべて０以下になりました（表５）。支配戦略はかわけん不参加、すなわち起業をやめろと言うことになります。一方、仲間のほうは少ないなりにも利益はあるようです。

かわけんはこの結果に愕然としました。「これって利益が半分になった時だよね。でも必ずしも半分になるわけではないよね。予定通りのときもあるし・・・」と思いました。このような場合は利益が通常の場合と、半分の場合の確率を使って混合戦略で分析します。ただし必ずしもこのどちらかになるとは限りません。

そこで利益がq倍になったらどうなるんだろうと変数を用いて計算することにしました（表６と７）

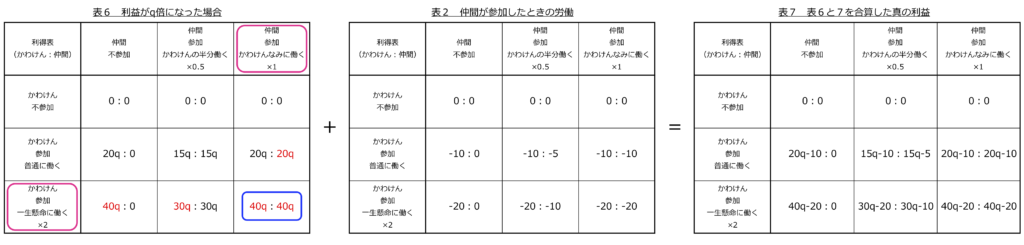
どうもかわけんの真の利益は、仲間の働き方によって変わってくるようです（表７）。かわけんなみに働いてくれて、かわけん１人でやってるのと同じ利益です。もし仲間が働きが半分ならかわけん利益が減ってしまいます。しかも仲間より利益が増えることは絶対なさそうです。
かわけんの利益がゼロになる損益分岐点を計算すると、仲間が半分働いてくれる時で30q-20=0を解いて2/3倍、仲間が自分なみに働いてくれる時で40q-20=0を解いて1/2倍となっています。最低でも予定利益の半分がないとかわけんの利益はマイナスに転落です。これはかなり厳しい条件です。かわけんは創業者なのにこれは洒落にならんと考えました。

次にかわけんは表３で、仲間の働きに関わらず仲間の利益は同じだったことを思い出しました。そこでもし仲間が参加だけして、全く働かなかったらどうなるかを計算することにしました（表８と９と１０）。

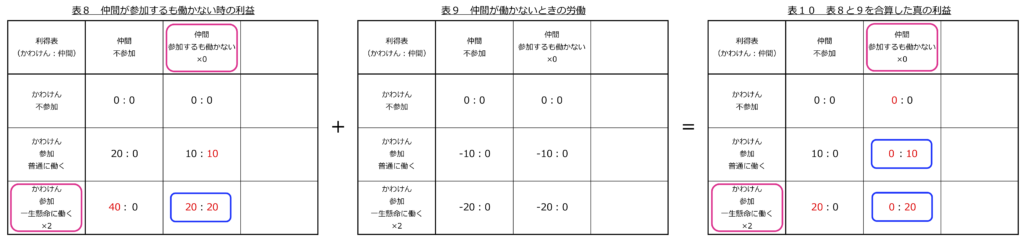
かわけんの支配戦略は一生懸命働く、仲間の支配戦略は参加して働かないです。ナッシュ均衡は２つ、支配戦略均衡は１つです。支配戦略均衡なので仲間はこちらを選びます。この表をよく見ると仲間の利得表は表３と全く同じです。すなわち仲間は働く量にかかわらず利益は同じです。
かわけんは愕然としました。

「これはたまたまでた数字に違いない、変数で計算しよう」と考え、仲間はかわけんのp倍働くとし計算しました（表１１と１２と１３）。

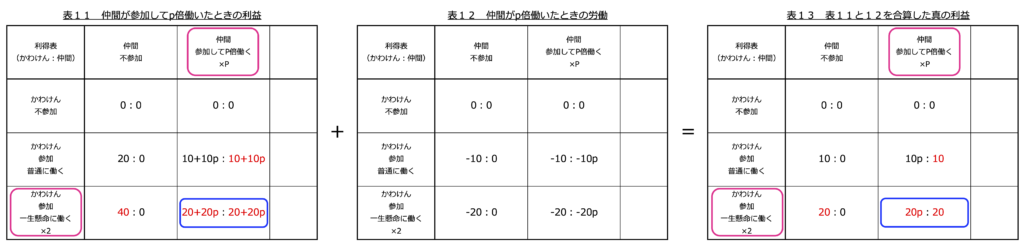
かわけんの支配戦略は一生懸命働く、仲間の支配戦略は参加してかわけんのp倍働くです。変数があるのでナッシュ均衡は決めにくいのですが、普通なら右下の１つです。支配戦略均衡になっています。
驚いたことに仲間の真の利益は変数pが含まれていません。せっかく働いてもらうためにインセンティブ契約をしたのに、仲間に関しては全くインセンティブになっていません。実は仲間は固定給だったんです。しかもかわけんの真の利益は変数pが含まれているので、仲間の働きに完全に左右されます。
こうなればpの値は明らかに０、働かないです。すなわち仲間は全く働かず固定給の利益を得て、かわけんは一生懸命働いて利益はゼロになりました。
かわけんは愕然とします。

そんな事はないだろうと思い、利益q倍、仲間の働きp倍で変数を2つ用いて計算しました（表１４と１５と１６）。

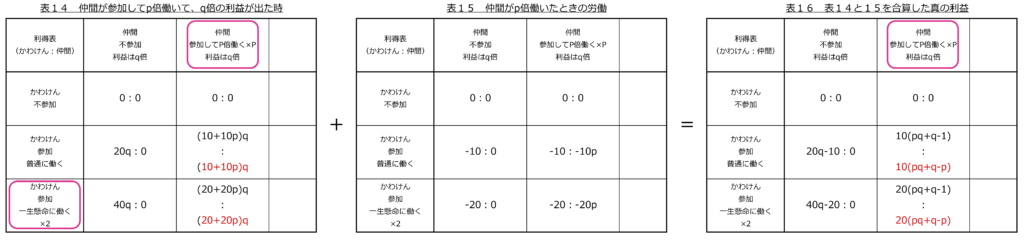
かわけんの支配戦略はなし、仲間の支配戦略は参加してp倍働くです。ナッシュ均衡はありません。
かわけんの基本的な変数はpq+q-1、仲間の基本的な変数はpq+q-pです。両者は最後が１かpかの違いです。pが１以上（かわけん以上に働く）ならかわけんの変数が大きくなりますが、先程の理屈でいくと仲間はp=0（働かない）を選ぶはずなので、絶対かわけんの変数のほうが小さくなります。変数はq-1になるので、かわけんは予定以上の利益を挙げなければ即利得0になる計算です。これは相当厳しい条件です。一方仲間は変数qになるので、少しでも利益があれば固定給がもらえます。

かわけんは絶望的な話だとおもいました。
ゲーム理論ではこのような場合、対処法がいくつかあります。
契約条件で一生懸命働くことを書く、本人にしっかり働くというコミットメントをさせる、悪い評価を立てられると困るだろうと脅す、などの手段を考えました。しかし経済学では完備契約はとても難しく不完備契約になるものとされています。コミットメントは裏付けがないとふりとの区別がつきません。仲間とは知り合ったばかりで、今後も付き合いはありませんので、評判は脅しになりません。したがってどれも難しい様です。

そこで、かわけんはゲーム理論を習得するメリットを思い出しました。それは相手に望ましい行動を取らせるためにゲームのルールを策定できるです。そう、最終手段はゲームのルールを変えることです。今回の設定は利益を均等に分ける、初期投資すべてかわけん、と言うことでした。このルールを変えればゲーム的状況は変わってきます。
じゃぁ、この利益分配比率をｒとして配分はｒ：１−ｒ、初期投資比率をｓとして投資分担をｓ：１−ｓに変えて計算・・・・・・・。

プシュー。かわけんはオーバーヒートしました。

そこでかわけんははっと気づきました。
そもそもかわけんが誘わなければ、仲間は参加しない！
このゲーム的状況の最初は交互手順で、同時手順ゲームではありませんでした。誘わなければ1人で起業すればいいだけの話です。
と言うことで、もう難しい計算はやめてかわけんは１人で起業することになりました。めでたしめでたし。

ゲーム理論を実際に適応してみました。かわけんの取るべき行動が明らかになりました。
ゲーム理論って、本当に役に立ちますよね。でも、疲れた・・・。

ここまでできれば、Step 3 実際の状況にゲーム理論を適用を実行したと言えるでしょう。すなわち、かわけんは「ゲーム理論を習得」しました。RPGならレベルアップですね。

５ゲーム理論の実際への適応・ネコと嫁さん１

起業の時、仲間を誘うかは悲しい結果になりました。お金が絡むだけに殺伐とした問題でしたね。
さて、ここからはもっと大事な現実の問題、最初に出した命題をゲーム理論で分析しましょう。ネコに好かれるかと、嫁さんから小遣いをもらえるか、です。
　

１ネコに好かれるか
ネコは決まった時間にご飯を貰います。ご飯をあげるのは、かわけんと嫁さんの仕事です。
ご飯の時にかわけんは撫でてあげますが、たまに嫌そうにみえることがあります。逆にかわけんが撫でようとしてネコが逃げると、かわけんは寂しくなります。一方、嫁さんは単に餌を上げるだけで、全然撫でたりしません。しかし見ていると、ネコはなんとなくかわけんより嫁さんのほうが好きそうに見えます。
かわけんはどうすればいいか知りたいと思っています。
これをゲーム理論で分析します。

ゲームの構成要素
・プレイヤー：かわけん、ネコ
・戦略：かわけんは「撫でない」「撫でる」。ネコは「撫でられない」「撫でられる」
・利得：利得表
ゲーム的状況：非協力、情報完備、短期間、同時手順

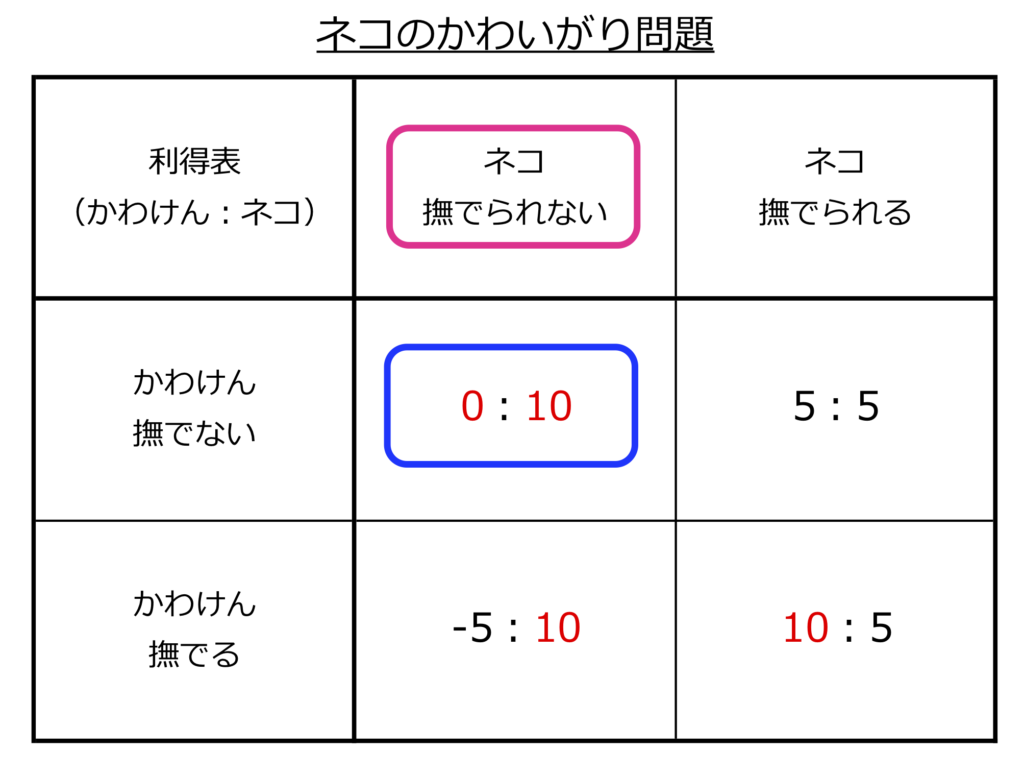
やっぱり予想通りの結果になりました。ナッシュ均衡は、かわけん「撫でない」とネコ「撫でられない」になります。かわけんの行動はナッシュ均衡に従っていませんでした。これでかわけんが嫌われ、嫁さんが好かれるわけがゲーム理論ではっきりしました。かなり悲しい結果ですね(T_T)。
ただしネコはゲーム理論の大前提である合理性のある人ではなく、気まぐれな非人間です。もしかしたら撫でられてご飯を食べるのが嬉しいかもしれません。それを期待して今後も撫で続けようと思います。
　

２嫁さんから小遣いをもらえるか
今度はお小遣いを嫁さんからもらう方法です。かわけんにとって、ネコよりこちらの命題が重要です。
これは家庭内のお金の移動になりますのでほぼゼロサムゲームになります。ただ、普通ならゼロサムゲームですが、家庭内の件なので感情が絡んでます。
嫁さんがくれないのに小遣いを奪い取ると機嫌をおおいにそこねます。また逆に、くれると言うのをもらわなければご機嫌になるかもしれません。機嫌はこれからの人生のこともあるのでとても重要なポイントです。
かわけんはお小遣いがもらえるか知りたいと思っています。
これをゲーム理論で分析します。

ゲームの構成要素
・プレイヤー：かわけん、嫁さん
・戦略：かわけんは「もらわない」「もらう」。嫁さんは「渡さない」「渡す」
・利得：利得表
ゲーム的状況：非協力、情報完備、短期間、同時手順

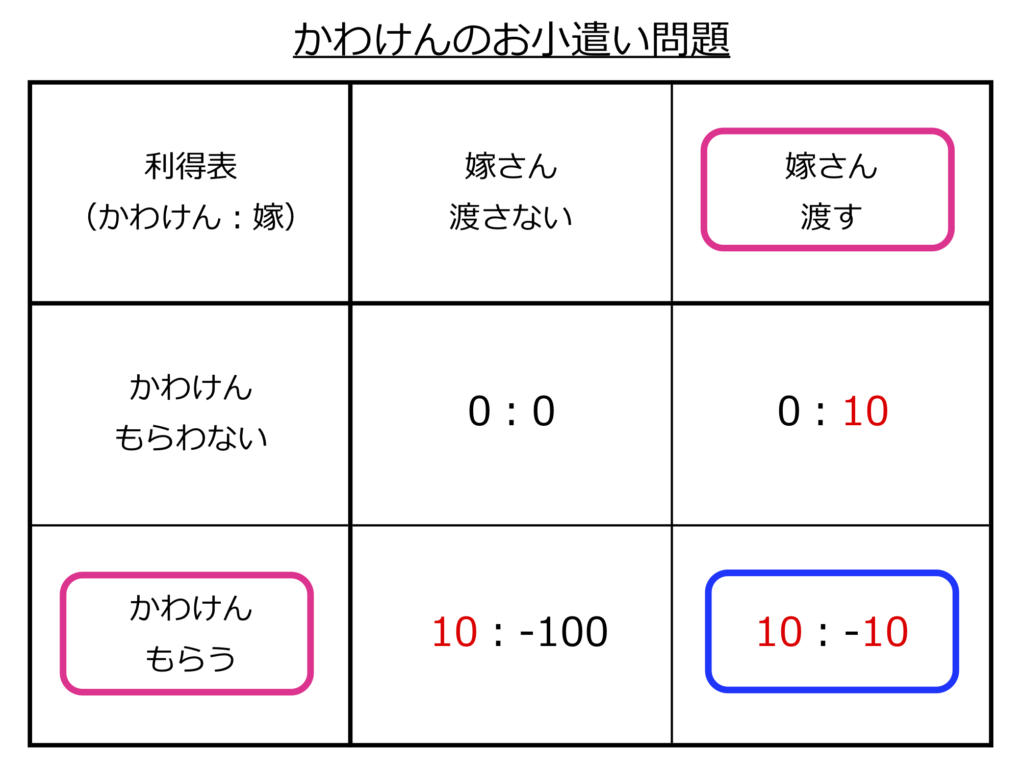
おお素晴らしい。かわけん「もらう」、嫁さん「渡す」がナッシュ均衡かつ支配戦略均衡になりました。理論上はお小遣いが絶対もらえるということです。とても望ましい結果ですね。

これから小遣いをほしいときは
かわけん：お金頂戴
嫁さん：なんで？
かわけん：ナッシュ均衡だから。ほら、この表見て！
嫁さん：・・・（ナッシュ均衡だから、渡すしかない）

こんな風に、これから小遣いが欲しい時はこの表を目の前に突きつけて、ナッシュ均衡だからくれ、と言うようにしましょう。これで無限にお小遣いを得る理論を手に入れましたね。
ただし問題は嫁さんはネコ同様に合理性のある人とは言いかねると言うことです。「くれ」と言うと「嫌」と言う返事が返ってくるのは目に見えてます。そんなときは、ちょっと表現を柔げて「ください」と言えばいいかもしれません。

さて、このパートでは見事に最初の命題をゲーム理論で分析することができました。しかも素晴らしい結果でしたね。
すなわち、かわけんは習得したゲーム理論を日常生活に拡張し、更にレベルアップ、「ネコに好かれるかもしれない方法（かなり不確実）」と「嫁さんから永久に小遣いを貰う方法（確実）」のアビリティをゲットしました。

６最後通牒ゲーム・ネコと嫁さん２

ここまでゲーム理論について色々と書いてきました。ゲーム理論は単一の意思決定では解決できない問題を理論化するために考えられてきました。それには人間が合理的であることが大前提になっています。もっとも経済学は人間が合理的であることを前提として成立する学問です。しかしどうしても人間は常に合理性ではありませんので、実際は異なる結果になることがあります。このような結果はアノマリーと呼ばれています。

そのようなアノマリーの代表が、最後通牒ゲームと呼ばれるものですです。

最後通牒ゲーム
「分配者（A）が、自分と相手（B）の取り分の分配額を提案し、BがAの提案を受け容れるか、拒否するかを選択する。BがAの提案を受け容れれば、両者ともそれぞれの分配額を得るが、BがAの提案した金額を拒否すると２人とも何ももらえなくなる」

望月文明 – 最後通牒ゲームにおける利他的な申し出への反応に関する一考察

身近な例で具体的に考えてみましょう。

ある日、神様がかわけんに1000円を渡しました。
そして「かわけん、1000円を渡すから嫁さんと分けるんだよ。嫁さんにあげる金額はかわけんに任せる。 ただ嫁さんが納得しなければ1000円は返してもらうから。」と言いました。

さて、皆さんはいくら渡します？

　

　

　

　

模範解答は、かわけん999円、嫁さん1円です。

びっくりするでしょう！
ただこの問題をゲームの状況として考え、利得表を書いてみれば理解できます

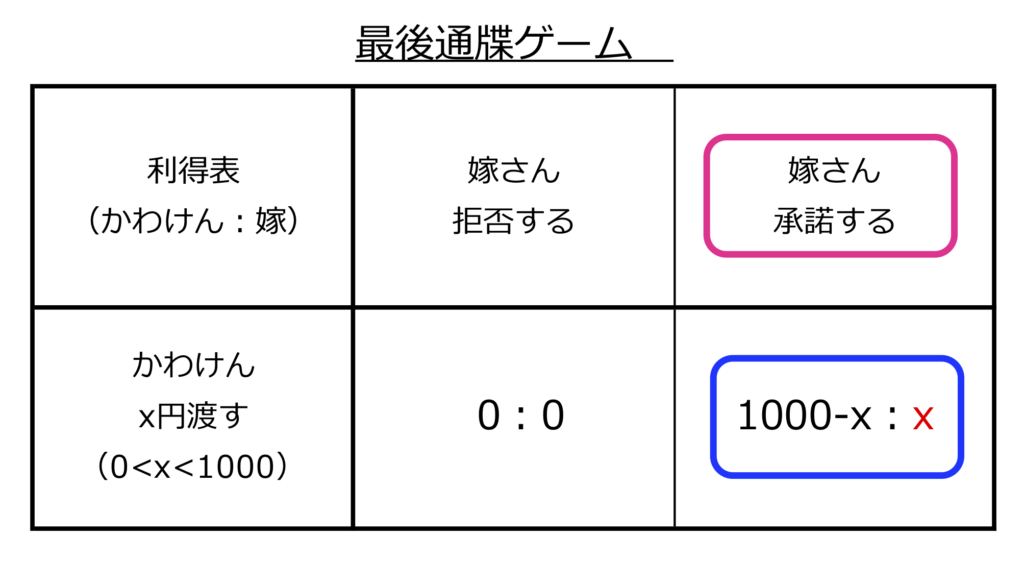
嫁さんが合理的な人間なら、拒否することなくx円を承諾します。ｘはかわけんが決めますから、かわけんが合理的なら1円（もしくは0円）にするはずです。したがってかわけん999円、嫁さんは1円が模範解答になります。
ただし現実的に考えるとこの提案は間違いなく拒否されます。うちならケンカになりますね。
この実験は世界中で行われており、国や文化よって金額は随分異なるようです。ちなみに日本では平均420円になるらしいです。
合理的な人間を自認するかわけんでも、0円ではなく最低でも420円以上を提案すると思います。もっともうちの嫁さんなら420円ということはありえず、最低で500円、下手したら700円以上を提案しなければ承諾しないかもしれません。しかし私のほうもそれに反撃する術がありません。
逆にかわけんが日頃の感謝の気持から800円を提案すると、嫁さんは「怪しすぎる。この人、ネコの餌やり当番を私だけに押し付けるつもりじゃ・・・」と拒否するかもしれません。実際、実験では高価格の提案は拒否される傾向にあるようです。
これら結果を見ると、どうも合理的な人間であるはずのかわけんも嫁さん合理的ではないようです。

この最後通牒ゲームは人間はいかに合理的でないかを示しており、この謎を突き止めていくためには、 人の持つ合理性とは何かと言う問題を考える必要があるとされています。

この最後通牒ゲームの研究結果は、伝統的な経済学やゲーム理論が示す意思決定とは全く異なるものです。このような不思議な行動は前述のようにアノマリーと呼ばれています。最終通帳ゲームはゲーム理論の最も代表的なアノマリーで、行動ゲーム理論と呼ばれています。
伝統的な経済学では理解できないことを説明するためゲーム理論が生まれ、ゲーム理論で理解できないアノマリーを説明するため、アノマリーに共通した特徴を調べる行動経済学、経済問題に対して実験的な手法による研究を行う実験経済学が生まれてきた様です。すなわちゲーム理論以降のどれもが、以前の理論では説明しきれない現実の世界を理解するために発展してきたといえるでしょう。

じゃぁ人間は合理的ではないんでしょうか？
もし合理的でないと仮定すると、経済学の最初の大前提が崩れてしまいます。そこで合理的あるという前提を置いたまま、現実社会の状態に合わせていろいろな理論が発展したようで、その中の1つのゲーム理論であるようです。
前述の問に対しては、「人間は絶えず合理的というわけではない、くらいの理解でいいんじゃないでしょうか」、と本には記載されていました。
　
　

さてもう一回、具体例で考えましょう。今度は嫁さんではなくネコです。

ある日、神様がかわけんにお刺身1000切れを渡しました。
そして「かわけん、お刺身1000切れをネコと分けるんだよ。ネコにあげる数はかわけんに任せる。 ただネコが納得しなければお刺身は返してもらうから。」と言いました。

さて、皆さんはいくつ渡します？

　

　

　

もちろんこちらも模範解答は、かわけん999切れ、ネコ1切れです。

じゃあ、ネコに1切れあげるとどうなるか。
もちろんネコは喜んで1切れを食べます。そして、かわけんが999切れを持っているのを羨ましそうに見て、「にゃー（もうちょっとくれ）」と言います。しかし「もうダメ」とかわけんが言ったら、諦めてトコトコどこかに行ってしまいます。
ネコは１切れを承諾する、すなわち模範解答どおりの行動です。なんと、驚くことにうちの嫁さんよりネコのほうが人の合理性を持っているんですよ。
現実は、「人間は合理的な人間ではないのに、ネコは合理的な人間」なんですよ。本当に不思議ですね。
　

そう考えると、その前の命題、５ゲーム理論の実際への適応・ネコと嫁さん１の答え、
「ネコは撫でないほうがいいが、人の合理性を持っていないので、撫でてもいいかもしれない」
「嫁さんは、人の合理性を持っているので、いつでもお小遣いをくれる」
は成り立たない気がします。

結論として家庭内の重要命題は
「ネコは人の合理性を持っているので、ゲーム理論に従って、撫でないほうがいい」
「嫁さんは人の合理性を持っていないので、ゲーム理論に従って、いつでもお小遣いをくれるとは限らない」
となりました。うーん、せっかく小遣いを無限にせしめる手段を得たと思ったのにとても残念です。

すなわち、かわけんはさらに行動ゲーム理論を習得したが、「ネコに好かれるかもしれない方法」と「嫁さんから永久に小遣いを貰う方法」のアビリティを失った、となりました。賢くなったけど、必殺技を失ってちょっと寂しいですね。

最後に

今日は経済学・経済政策の中から、ゲーム理論を取り上げてお話しました。
楽しんでいただけたでしょうか？

ここで、ちょっと今回のブログの注意点です。
４ゲーム理論の実際への適応・起業編で行った利得表の合算は、正式な手段かは全然知りません。かわけんのオリジナルです。基本的には利得表の中は相対値なので、合算はダメかも知れませんが、現実世界に合わせて理解しやすいように足してみました。
また、５ゲーム理論の実際への適応・ネコと嫁さん２の小遣いを貰う方法は、実は交互手順ゲームで時間不整合性の要素が入っています。正確とは言い難いので、決して家庭内で濫用しないでくださいね。
後半はブログを面白くするために、都合の良い解釈が入っていますので参考にされるときはご注意ください。

私は診断士試験までは経済学について勉強したことは全然ありませんでした。ちょうど２年前の１２月頃に初めてスピードテキスト経済学・経済政策を読み始めました。もちろん、ゲーム理論が何たるかは全く知りませんでした。
それが２年後の今、こうやってゲーム理論に関する長文ブログを書くようになりました。今回、ブログのために３週間くらいゲーム理論についてどっぷり勉強しました。随分本を読みましたが、バックグランドして経済学の知識があるので理解も早くとても楽しかったです。これは２年前には全く予想できなかった状況で、人生とはわからないものだと感じています。こんな面白い世界を垣間見ることができたとき、本当に診断士の勉強をしてよかったと思います。
ただあくまでズブの素人の独学です。もし受験生やタキプロのメンバーで詳しい方がおられましたら、いろいろ教えて下さい。そうしていただければ、また自分の世界を広げることができますね。

さて今回のブログで私が勉強の話を書くのは終わり、後は「号外編・エッセイ」、「合格後の活動」、「最後に伝えたいこと」の３回です。だからこれで私が人生でもう経済学を勉強する事はないでしょう。ただ、今回の勉強で得た知識と面白さをこれからも活かしていきたいと思います。
今回のブログのような内容は、どうしても時間に追われていた受験生時代には、ゆっくり考えることが出来ませんでした。しっかり勉強してアウトプットするのは面白いです。
タキプロに入りブログ班に所属したからこそ、このような機会を得ることができました。
本当にタキプロに参加してよかったです！

受験生の皆さんも、合格されたら、ぜひタキプロに参加してくださいね。
皆さんの加入を、１２期一同心から楽しみにしています。
　

「えー、入るかわからない！？」
そうゆう人はゲーム理論で分析してください。
ナッシュ均衡、支配戦略均衡、パレート効率の全部が一致して戦略は参加
になるはずですから！
　

最後まで長文を読んでいただきありがとうございました。かわけんでした。
次回は、うららさんの登場です。
お楽しみに！

最後まで読んでいただき、ありがとうございます！
↓下のボタンを押して、読んだよ！ と合図していただけると、とっても嬉しいです。
（診断士関連ブログの人気ランキングサイトが表示されます[クリックしても個人は特定されません]）

にほんブログ村

皆様の応援がタキプロの原動力となります。
ぽちっと押して、応援お願いします♪

皆様の応援がタキプロの原動力となります。
ぽちっと押して、応援お願いします♪