ゆる統計×機械学習 byにゃーもん

タキプロ15期の にゃーもん と申します。
タキプロ16期メンバー募集
★参加応募受付中★
下記バナーから参加申し込みいただけます!
■受験生現役時代と統計
1次試験本番でも統計はわかんないと思いながら解いてましたし、実際全然理解してませんでした。ですが、合格後時間ができてようやく朧げながら理解できてきたので今回の記事のテーマにしたいと思います。
診断士合格後思うところあってDS検定の勉強をしていて、「あーこの論点が1次試験の段階で飲み込めてればなあ」と思うことが多々ありました。統計の資格といえば統計検定が有名ですが、最近IT関係の技術と絡めたG検定やDS検定も人気のようです。
統計についてはタキプロで過去にも解説記事のシリーズがあります。
こちらもよければご覧ください。
あおきの統計学入門その1 #10 by あおき さん
■統計は捨て問、だけど
近年の傾向では、経営情報システムにおいて毎年統計問題が2問程度出題されますが、難易度が高い割に配点が少ないため捨て問でよいという話が多いです。私もそう思います。統計問題2問正解で8点とるなら、他の論点を固めて8点取ったほうがコスパがいいと思います。
しかし、統計が理解できると機械学習への解像度が上がって相乗効果があるので、AIやマシンラーニングが盛んになってきた世の流れを鑑みてこのテーマを選んでみました。出題された時この記事のことをちょっとでも覚えていて、得点できたらラッキー、ぐらいに思ってください。統計は深追い厳禁というのは百も承知ですが、当記事はイメージが掴める程度のゆるゆるな説明と語呂合わせで進めます。
運営管理や事例Ⅳでも平均や標準偏差を使うので、その辺りは読者の皆様も手を動かして覚えていらっしゃる方も多いかと思います。その辺は端折って一足跳びに機械学習と親和性の高い論点から解説します。
■回帰と分類
まず分類はわかる気がするけど、回帰ってなに???統計でよく出てくるけどなんの話?
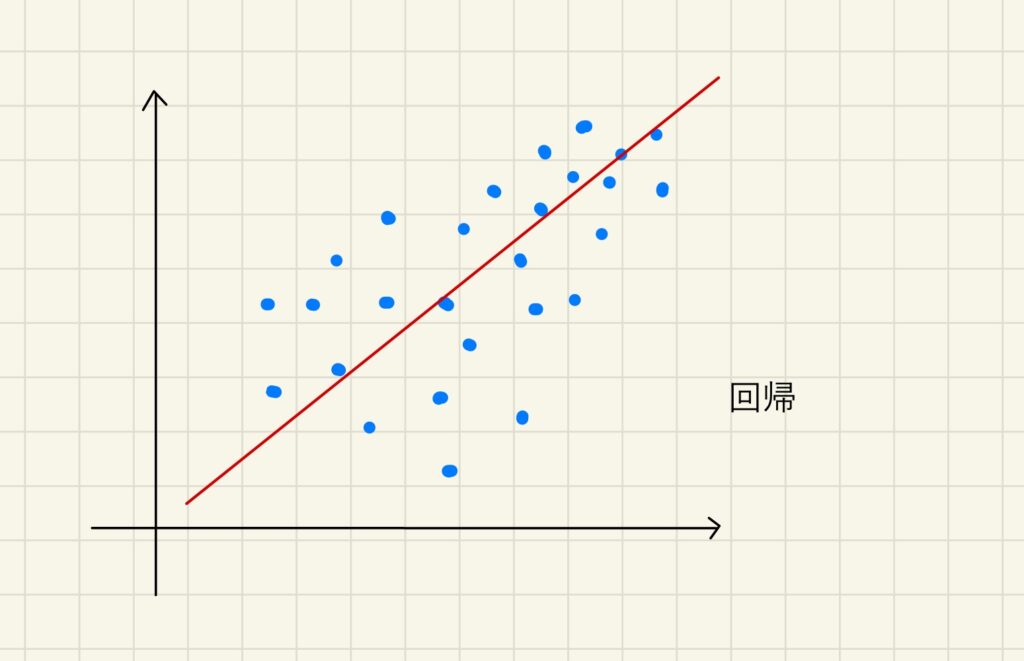
回帰というのはズバリ下図の赤い線のイメージです。モデル群の中に共通する平均的な性質や傾向を表します。
単回帰分析であればy=ax+bというような直線で表されます。重回帰分析ではy=ax+bu+cといったように2つ以上の変数が結果に影響するという式になります。(重回帰分析は平面のグラフで表すことは困難です。)
例えば、成人の身長と体重の平均グラフのようなものです。平均的な人より極端に太めな人、痩せ気味な人も集団内に存在するものの、回帰分析を行えば「身長が高い人は体重も重い」という規則性が見えてくると思います。
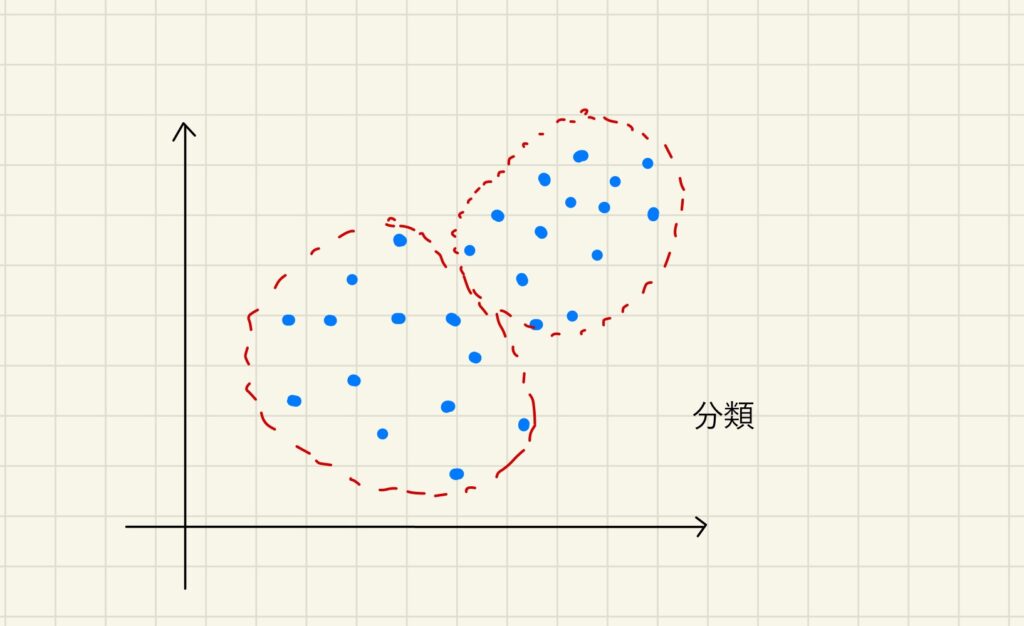
対して、分類は次の図です。モデル群を2つ以上のカテゴリに分けることです。こんなイメージ。集団内でデータの距離の近いなどの似たもの同士をグルーピングします。代表的なものはクラスター分析です。
でも、回帰ってちょっと不便なところがあります。身長についてグラフ化することはできますが、身長を「高い」「低い」と分類することが難しいのです。線形のグラフを書いて、どこからが「高い」のか「低い」のか表すにはどのようにしたらよいでしょう。
そんな時は分類も可能な「ロジスティック回帰」を使いましょう。わかりやすくするため、身長180cmなら「高い」、身長145cmなら「低い」と必ず判定されると仮定します。(説明のための極端な例ですので、数字自体に意味はありません。念のため)
もしこうしたモデルなら、身長190cmなら120%「高い」と判定されるのでしょうか?カンストしている場合の判定もわざわざするのは骨が折れます。「高い」か「低い」かという情報以外重要でない場合、シグモイド関数により予測します。シグモイド関数が何かと真面目に考えると難易度が跳ね上がるので、下図のように「回帰分析のグラフのカンストした両端をえいっ!とS字に曲げちゃうこと」と捉えてください。カンストしたものは0(低い)か1(高い)で分類されます。
下図のようなグラフであれば、180cm以上が「高い」、145cm以下が「低い」と正しく効率的に分類されます。145〜180cmの間の身長であれば、身長が180cmに近いほど「高い」と判定される可能性が高く、145cmに近いほど「低い」と判定される可能性が高いと言えるでしょう。(←すごくあたりまえといえばあたりまえな結論ですね)
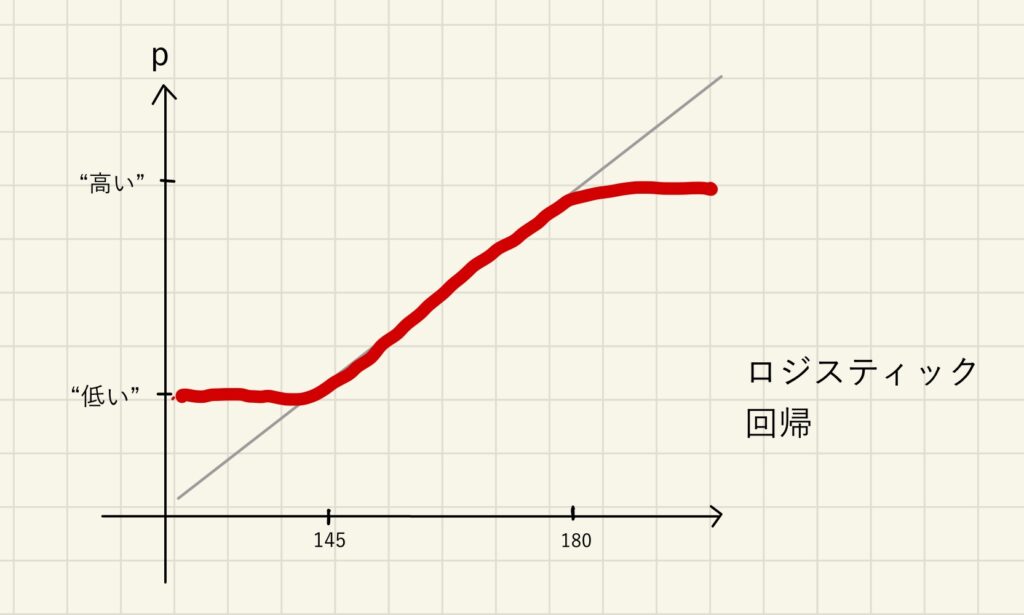
本来直線グラフ(灰色)になるはずですが、赤線のように曲げてます。
■回帰と分類の評価
回帰や分類にも出来のよいものとそうでないものがあります。それぞれ出来のよさを評価する方法が異なります。
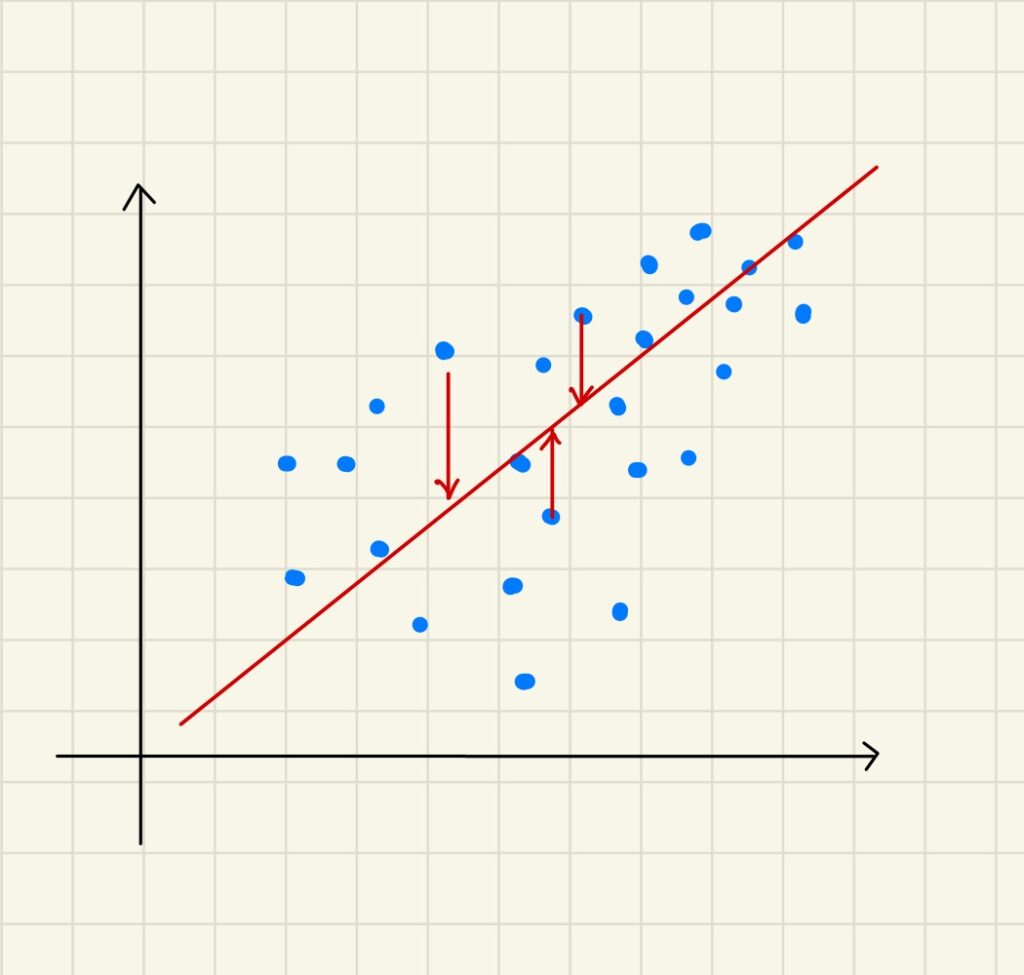
回帰では、「実績値と回帰モデルの予測値の差が小さい」ほど良いとされます。どう言うことかと言うと、下図は直線(予測値)と点(実績値)の差を赤い矢印で表しています。この赤い矢印の距離が短ければ短いほど良いモデルというイメージです。この赤い矢印は、具体的にはMAPEやMSEといった指標に対応します。
対して、分類は良し悪しを適合率や再現率といったもので評価します。つまり、せっかく分類するのに「偽陽性(FP)」や「偽陰性(FN)」が多い場合は良いモデルといえないと判断します。偽陽性や偽陰性が発生する理由は、分類する領域が被っているからです。下図の分類モデルの中の灰色部分を小さくして重なる部分を減らしていくことで正確な分類モデルになる、とイメージしてください。
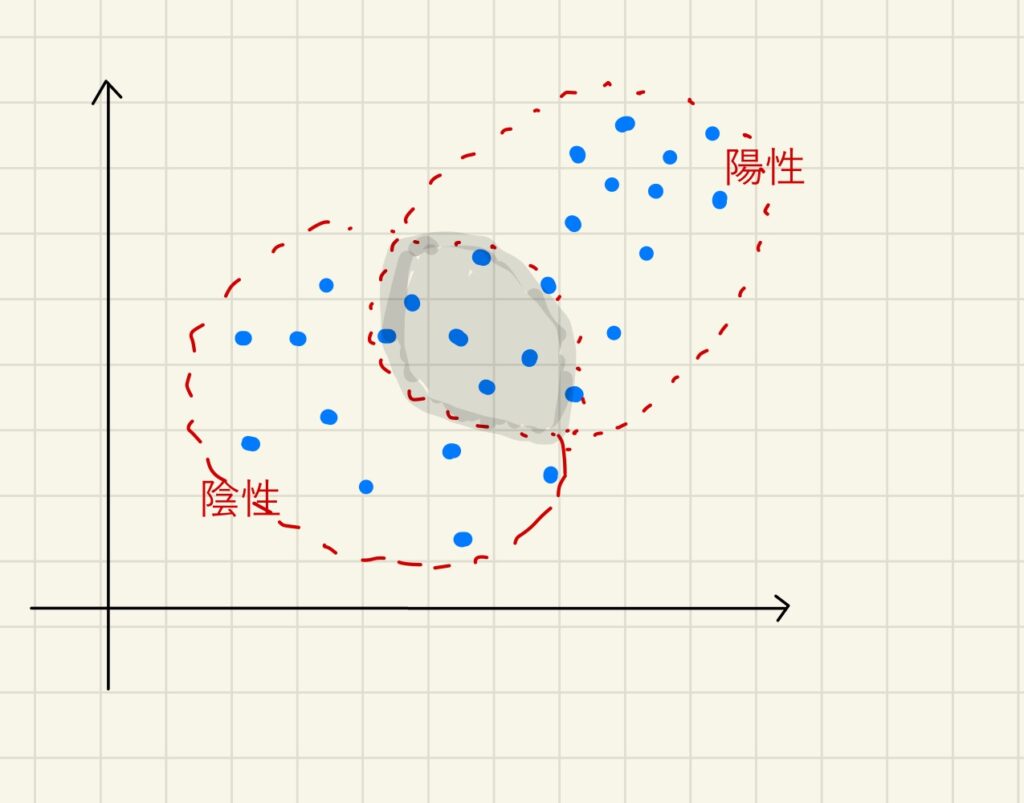
分類の評価法については令和5年問24にも出題がありました。
■検定力
統計的にある仮説を証明したい場合の手法を「検定」といいます。
証明したい仮説(対立仮説)とその逆の仮説(帰無仮説)を立て、逆の仮説(帰無仮説)を否定するというのが検定の流れです。検定の際に誤った結論を導いてしまうパターンとして「第1種の誤り」「第2種の誤り」があげられます。
第1種の誤り
帰無仮説が正しいときに、これを棄却してしまう誤りを第1種の誤り (Type I error) という。第1種の誤りを犯す確率を α で表す。α を危険率とも呼び、有意水準に等しい。
(中略)
第2種の誤り
誤った帰無仮説を棄却しない誤りのことを第2種の誤り (Type II error) という。第2種の誤犯す確率を β で表す。1 − β を検定力また検出力 (power) と呼び、誤った帰無仮説を正しく棄却できる確率を表す。
https://ja.m.wikipedia.org/wiki/仮説検定
初見ではなんのこっちゃ!?の論点ですが、ちゃんと語呂合わせがあります。
一種過誤をα過誤(α error)やあわてものの誤り、第二種過誤をβ過誤(β error)やぼんやりものの誤りとも呼ぶ。
https://ja.wikipedia.org/wiki/第一種過誤と第二種過誤
あ(α)わてものの誤りとは、例えば降水確率が高いが結局降らなかった日に傘を買ってしまう過誤のことです。
対して、ぼ(β)んやりものの誤りは、降水確率が高くて雨が降った日に傘を買わずに雨に降られてしまう誤りと言えるでしょう。
この場合対立仮説と帰無仮説は以下のとおり。
対立仮説:雨が降る
帰無仮説:雨が降らない
検定力(1-β)はこの例えで言うなら「雨が降る時に傘をちゃんと買っておく」ことと言えるでしょう。仮説が正しい時にぼんやりせずにちゃんと行動に移す力と言えるかもしれません。
自分としては下記のサイトの例えがすごくわかりやすかったので、引用させていただきます。
https://best-biostatistics.com/hypo_test/error.html
- 投資すると決めた結果、株価が値下がりした場合は、あわててしまったエラーですね。
- 投資しないと決めた結果、株価が値上がりした場合には、ぼんやりしていたエラーですね。
■ようやくマシンラーニング
回帰やら分析やらを用いて、コンピュータに自律的に計算させるのがいわゆる機械学習(マシンラーニング)です。
正解となるデータを与えて学習させる「教師あり学習」と、データだけ与えてパソコン自身に法則性を見つけさせる「教師なし学習」があります。さらに、パソコンの演算結果に応じて報酬を与え、報酬最大化するようにパソコンに試行錯誤させ学習させる「強化学習」があります。
代表的なものは以下のとおりです。線形回帰・ロジスティック回帰が教師あり学習に入ってますが、教師あり=回帰・教師なし=分類というわけではなく、教師あり学習は回帰も分析も両方の手法を使うことがあります。
教師あり学習(正解データを与える)
線形回帰
ロジスティック回帰
ランダムフォレスト
決定木
教師なし学習(正解をコンピュータが考える)
クラスタリング
強化学習(演算結果に応じて報酬を与える)
モンテカルロ法
Q学習法
生物の神経回路を模したとされるモデルにニューラルネットワークがあります。似ているものにディープラーニングもありますね。「ニューラルネットワーク」は入力層・中間層(隠れ層)・出力層の3層構造ですが、「ディープラーニング」は中間層を多層にすることでより高度で抽象的な判断を可能にするという違いがあります。
■おわりに
最初真面目に表計算ソフトでグラフをちまちま作ってましたが、あまりにしんどいのでiPadのノートアプリ(Goodnotes5)に手書きしたグラフを延々載せての解説となりました。お見苦しいグラフとなりすみません。
1次試験は4択問題なので、ちょっとしたことで選択肢を切ることができれば意外と得点につながります。皆様にゆるーく覚えてもらって得点につながるようであれば幸いです。
次回は、うなぽん さんの登場です。
お楽しみに!
最後まで読んでいただき、ありがとうございます!
↓下のボタンを押して、読んだよ! と合図していただけると、とっても嬉しいです。
(診断士関連ブログの人気ランキングサイトが表示されます[クリックしても個人は特定されません])

皆様の応援がタキプロの原動力となります。
ぽちっと押して、応援お願いします♪



