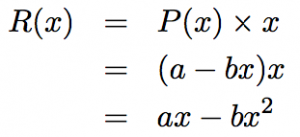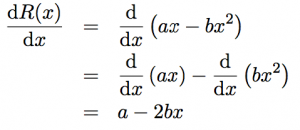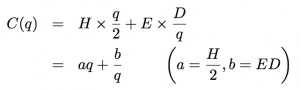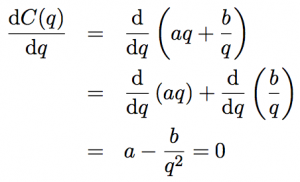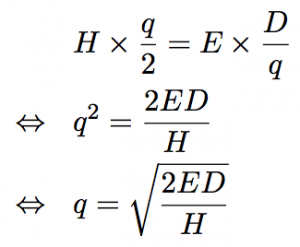[1次2次] 理系のための診断士学習法(#3:微分の活用)
中小企業診断士を目指す皆様、おはようございます。がんちゃん/岩間です。
診断士試験の学習過程では、色々な数式や数学的概念が出てきます。先週に引き続き、今週も、診断士試験向けテキストや予備校の講義では省略されがちの内容を見てみます。
今回は、微分の活用について見てみます。微分の活用法の一つは、関数の最大値・最小値を求めることです。この活用法を、診断士試験に出てくる概念で見てみます。
※先週までの内容:
- #1 (12/15)
- 1.[財務] DCF法の公式(簡易版)
- 2.[財務] DCF法の公式【数列】
- 3.[経済] コブ・ダグラス型生産関数の成長方程式/全要素生産性(TFP) 【対数・微分】
- #2 (12/22)
- 4.[経済] 微分の公式
- 微分に関して押さえておくべきこと(診断士試験の範囲)
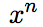 を微分すると、なぜ
を微分すると、なぜ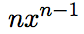 になるのか?
になるのか?
- 4.[経済] 微分の公式
◆目次
- 5.[経済・運営管理] 微分の活用
- 競争企業の利潤最大化
- なぜ利潤最大化の必要条件が「限界費用と価格Pとが一致すること」なのか
- 独占企業の利潤最大化
- (1)なぜ利潤最大化の必要条件が「限界費用と限界収入とが一致すること」なのか
- (2)なぜ需要曲線が直線の場合に限界収入曲線が傾き2倍の直線になるのか
- 経済的発注量
- 競争企業の利潤最大化
◆競争企業の利潤最大化
まずは、経済学で学習する「競争企業が利潤を最大化するための条件」を見てみます。
|
【知識:競争企業の利潤最大化条件】
※このことを「プライステイカー」と呼びます。 |
それでは、なぜ「限界費用と価格Pとが一致する(ように生産量xを決める)と利潤が最大化するのか」を考えてみます。
【方針】利潤を生産量xの関数として表し、次にその関数を微分することにより、利潤最大化の条件を求めます。
1.利潤をπ(x)とおいて、利潤π(x)を式で表します。
π(x)=Px–C(x) ・・・(1)
- ここで、C(x)は、その企業特有の費用関数とします(つまり、「その企業が物を○個作ったら、費用がいくらかかるか」を表す関数です)。
- 上記の式になる過程は、利潤π(x)は収入から費用を減じたものであり、その収入は「価格P×生産量x」で表されるからです。
2.利潤π(x)を微分します。
dπ(x)/dx=P–MC(x) ・・・(2)
- ここで、MC(x)は、限界費用関数とします。
- 上記の式になる過程は、次のとおりです。
- Pxを微分すると、Pになります。前回の記事で説明した「
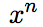 を微分すると
を微分すると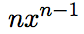 になる」という式を使います。
になる」という式を使います。 - 費用関数C(x)を微分した関数は、限界費用関数MC(x)です。
- Pxを微分すると、Pになります。前回の記事で説明した「
3.微分した関数(dπ(x)/dx) を0とおきます。
もともとの関数π(x)が最大化するとき、微分した関数 dπ(x)/dx はちょうどゼロになります(π(x)が最大化するときには、π(x)は増えても減ってもいない状態だからです)。そこで、2で求めた関数(式(2))を0とおきます。
P–MC(x)=0
⇔ P=MC(x) ・・・(3)
すなわち、「利潤π(x)が最大化するときは、価格と限界費用が等しい」といえます。
※少々高度になりますが、これまでに設定した前提だけからは、必要条件と言うのが限界で、十分条件とは言えません(すなわち「価格と限界費用が等しいときに、必ず、利潤が最大化する」わけではありません)。最小化する場合もあり得ますし、局所的に最大あるいは局所的に最小となっている場合もあり得ますし、さらに言えば、それらのいずれでもない場合もあります。
◆独占企業の利潤最大化
次は「独占企業が利潤を最大化するための条件」を見てみます。
|
【知識:独占企業の利潤最大化に関する事項】
※このことをプライスメイカーと呼びます。 |
ここでは、次の2点を見てみます。
- なぜ、限界費用と限界収入とが一致するように生産量xを決めると、利潤が最大となるのか
- なぜ、需要曲線が直線の場合に、限界収入曲線が傾き2倍の直線になるのか
1.なぜ限界費用と限界収入とが一致するように生産量xを決めると、利潤が最大となるのか
【方針】先ほどの競争企業の場合と同様、利潤を生産量xの関数として表し、次にその関数を微分することにより、利潤最大化の条件を求めます。
まず、利潤をπ(x)とおいて、利潤π(x)を式で表します。
π(x)=R(x)-C(x) ・・・(1)
- ここで、C(x)はその企業特有の費用関数、R(x)は収入関数とします。
次に関数π(x)を微分します。
dπ(x)/dx=MR(x)-MC(x) ・・・(2)
- ここで、MR(x)は限界収入関数、MC(x)は限界費用関数とします。
次に微分した関数を0とおきます。
MR(x)-MC(x)=0
⇔ MR(x)=MC(x) ・・・(3)
すなわち、「利潤π(x)が最大化するときは、限界収入と限界費用が等しい」といえます。
(ここまでの議論は、競争企業であっても成り立ちます。つまり、競争企業でも、「利潤最大化条件は限界収入と限界費用が等しいとき」と言えます。先ほど求めた競争企業における条件では、収入R(x)を具体的にPxとおいて求めました。)
2.なぜ、需要曲線が直線の場合に、限界収入曲線が傾き2倍の直線になるのか
【方針】需要関数を数式で表す→収入関数を求める→限界収入関数を求める、という順で求めてみます。
まず、需要関数P(x)を式で表します。需要曲線が直線であることから、定数2つを用いて、![]() と表せます。
と表せます。
すると、収入関数R(x)は、次のようになります。
限界収入関数は、収入関数R(x)を微分することで求められ、次のようになります。
◆経済的発注量
経済的発注量は、1次の運営管理の範囲で学びます。
|
【知識:経済的発注量】
|
ここでは、「なぜ在庫費用=発注費用となるときに、在庫に関連する費用が最小化するか」を見てみます。
【方針】在庫関連費用をC(q)として表し、それを微分することによって、C(q)を最小化する条件が「在庫費用=発注費用」であることを見ていきます。
1.まずは、年間の在庫関連費用C(q)を求めます。
在庫関連費用には、在庫費用と発注費用があります。それぞれ求めます。
年間の在庫費用は、「在庫1単位当たりの年間の在庫費用 H」と「平均在庫量 q/2」の積 H×q/2 で表されます。
年間の発注費用は、「発注1回あたりの発注費用 E」と「発注回数」との積で表されます。ここで、発注回数は、「年間の需要D」を「発注量 q」で割って求めます。従って、年間の発注費は E×D/q です。
これらから、年間の在庫費用C(q)は次のようになります。
2.次に、年間の在庫関連費用C(q) を微分し、0とおきます。
- b/qの微分は、b×(qのマイナス1乗) と考えて行います。
3.この条件式を少し変形すると、「在庫費用=発注費用」となります。
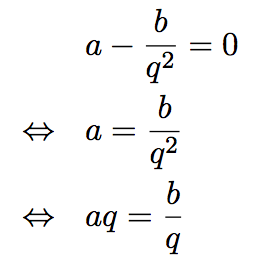 試験対策としては、「在庫費用=発注費用」であることを記憶しておき、下記のように、「在庫費用=発注費用」と立式し、qを求めるようにすると良いです。
試験対策としては、「在庫費用=発注費用」であることを記憶しておき、下記のように、「在庫費用=発注費用」と立式し、qを求めるようにすると良いです。
年末になり、1年間を振り返っている方も多いと思います。人それぞれ良いことも悪いこともあったことと思いますが、まずは「1年間通して目標に向けて継続的に努力されてきたこと」に注目するのをお勧めします。そうすることで、振り返り+次期への改善を、前向きに進められるからです。
どうぞ良いお年をお迎えください。
以上、がんちゃん/岩間でした。
タキプロ 実務補習セミナーのお知らせ
【東京】
■日時・定員・申込:
① 2015年1月12日(月・祝)定員:40名
セミナー:14:00~16:30(13:30開場)
懇親会:17:00~19:30頃
お申し込みはこちら
② 2015年1月14日(水)定員:30名
セミナー:19:00~21:30(18:30開場)
懇親会:21:30~23:00頃(途中退出自由)
お申し込みはこちら
~両日共通~
■会場:日本橋公会堂(中央区日本橋蛎殻町一丁目31番1号)
■対象者:2次試験合格(見込み)者
■参加費:無料(懇親会3,500円程度)
■内容:
診断士登録までの道のりは?
実務補習ってどんなことするの?
事前準備はどうすればよい?
身に着けておきたいITスキルは?
※①、②とも同内容のセミナーとなっています。
ご都合に合わせてご参加ください。
お問い合わせ先:タキプロ事務局 takipro2010@gmail.com
【名古屋】
■日時:1月12日(月・祝) 14:30~16:30(14:00開場)
■会場:昭和生涯学習センター
■対象者:2次試験合格者
■定員:10名
■内容:実務補習についてのガイダンス
「実務補習ガイダンス」と「実務補習のためのIT講座」
■参加費:無料 (懇親会3,500円程度)
■お申し込み:こちら
お問い合わせ先:takipronagoya@gmail.com
====================